# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -5781. 306. -18.9 5.59e- 55
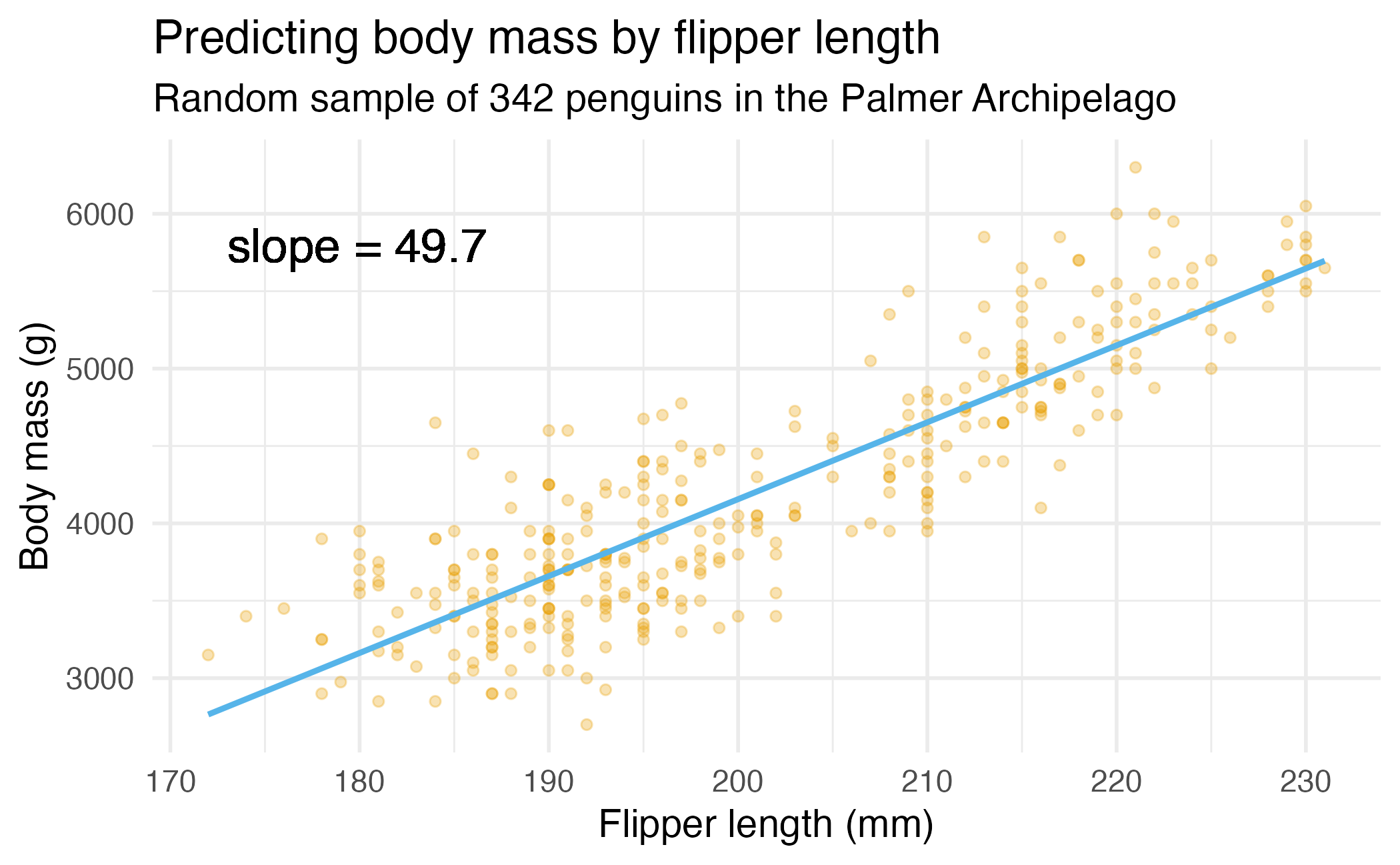
2 flipper_length_mm 49.7 1.52 32.7 4.37e-107Quantifying uncertainty with bootstrap intervals
Lecture 21
Cornell University
INFO 2950 - Spring 2024
April 11, 2024
Announcements
Announcements
- Lab 05
- Homework 06
- Preregistration of analyses
Goals
- Quantify uncertainty around parameter estimates
- Implement bootstrap resampling methods
- Calculate and interpret confidence intervals
Recap and motivation
Remember the penguins
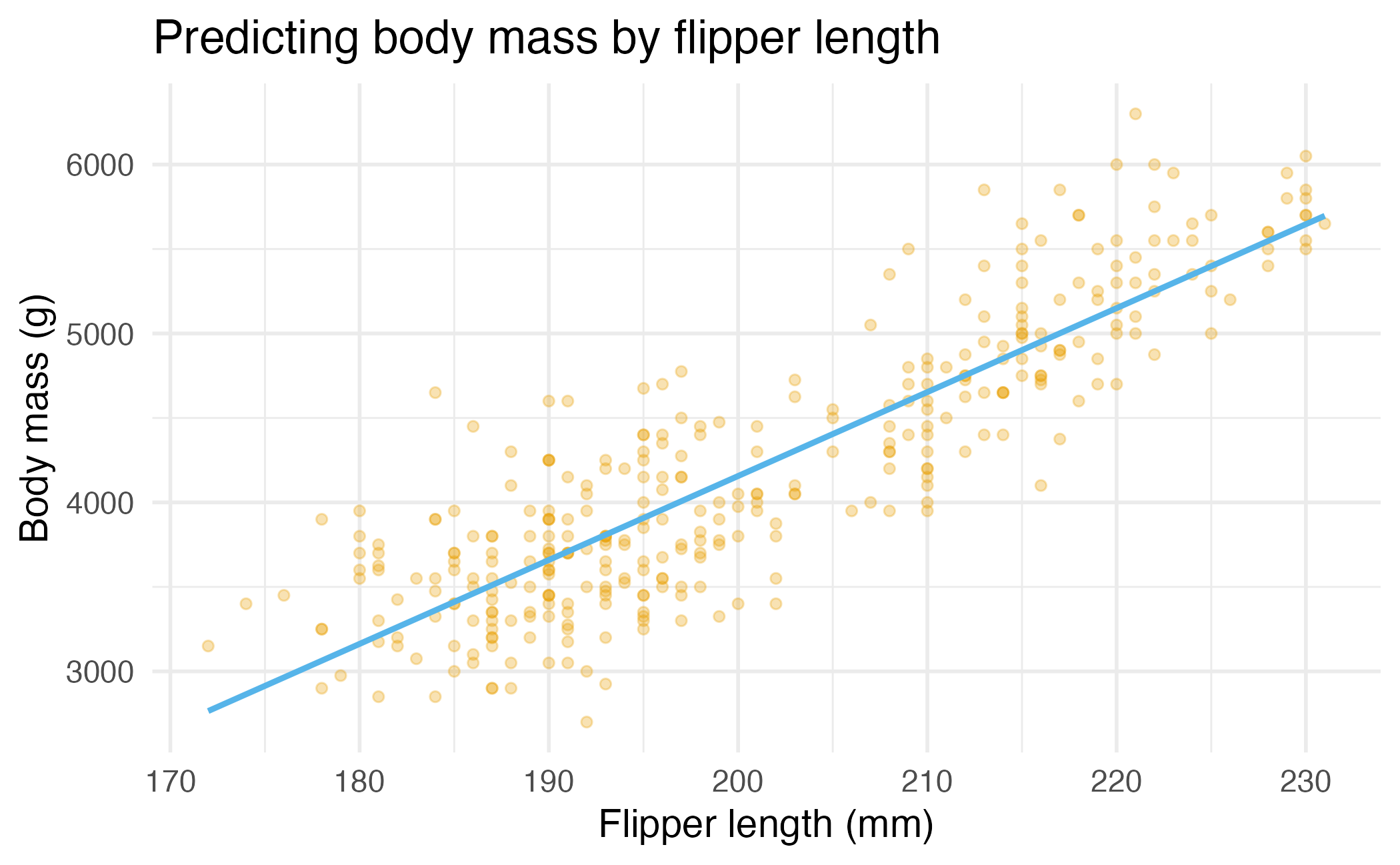
\[ \widehat{\text{body mass}} = -5781 + 49.7 \times \text{flipper length} \]
What does this line tell us?
Remember the penguins
\[ \text{body mass} = \beta_0 + \beta_1 \times \text{flipper length} \]
- What is \(\beta_1\)?
- Does our estimated line tell us what \(\beta_1\) is?
Inference
Statistical inference
… is the process of using sample data to make conclusions about the underlying population the sample came from
Estimation
- Use data from samples to calculate sample statistics (mean, median, slope, etc.)
- Which can then be used as estimates for population parameters
Hypothesis testing
- Use data from samples to calculate \(p\)-values
- Which can then be used to evaluate competing claims about the population
If you want to catch a fish, do you prefer a spear or a net?


If you want to estimate a population parameter, do you prefer to report a range of values the parameter might be in, or a single value?
- If we report a point estimate, we probably won’t hit the exact population parameter
- If we report a range of plausible values we have a good shot at capturing the parameter
- Election forecasts
- Approval polling
Confidence intervals
Confidence intervals
A plausible range of values for the population parameter is a confidence interval.
- In order to construct a confidence interval we need to quantify the variability of our sample statistic
- For example, if we want to construct a confidence interval for a population slope, we need to come up with a plausible range of values around our observed sample slope
- This range will depend on how precise and how accurate our sample mean is as an estimate of the population mean
- Quantifying this requires a measurement of how much we would expect the sample population to vary from sample to sample
Suppose we split the class in half down the middle of the classroom and ask each student their heights. Then, we calculate the mean height of students on each side of the classroom. Would you expect these two means to be exactly equal, close but not equal, or wildly different?
Suppose you randomly sample 50 students and 5 of them are left handed. If you were to take another random sample of 50 students, how many would you expect to be left handed? Would you be surprised if only 3 of them were left handed? Would you be surprised if 40 of them were left handed?
Quantifying the variability of slopes
We can quantify the variability of sample statistics using
- simulation: via bootstrapping (now)
or
- theory: via Central Limit Theorem (review your stats class and chapter 13)
Warning
These techniques assume that the sample is representative of the population of interest. If that is not the case, the results may not be valid.
Bootstrapping
Bootstrapping
- “pulling oneself up by one’s bootstraps”: accomplishing an impossible task without any outside help
- Impossible task: estimating a population parameter using data from only the given sample
- Note: Notion of saying something about a population parameter using only information from an observed sample is the crux of statistical inference
🥾
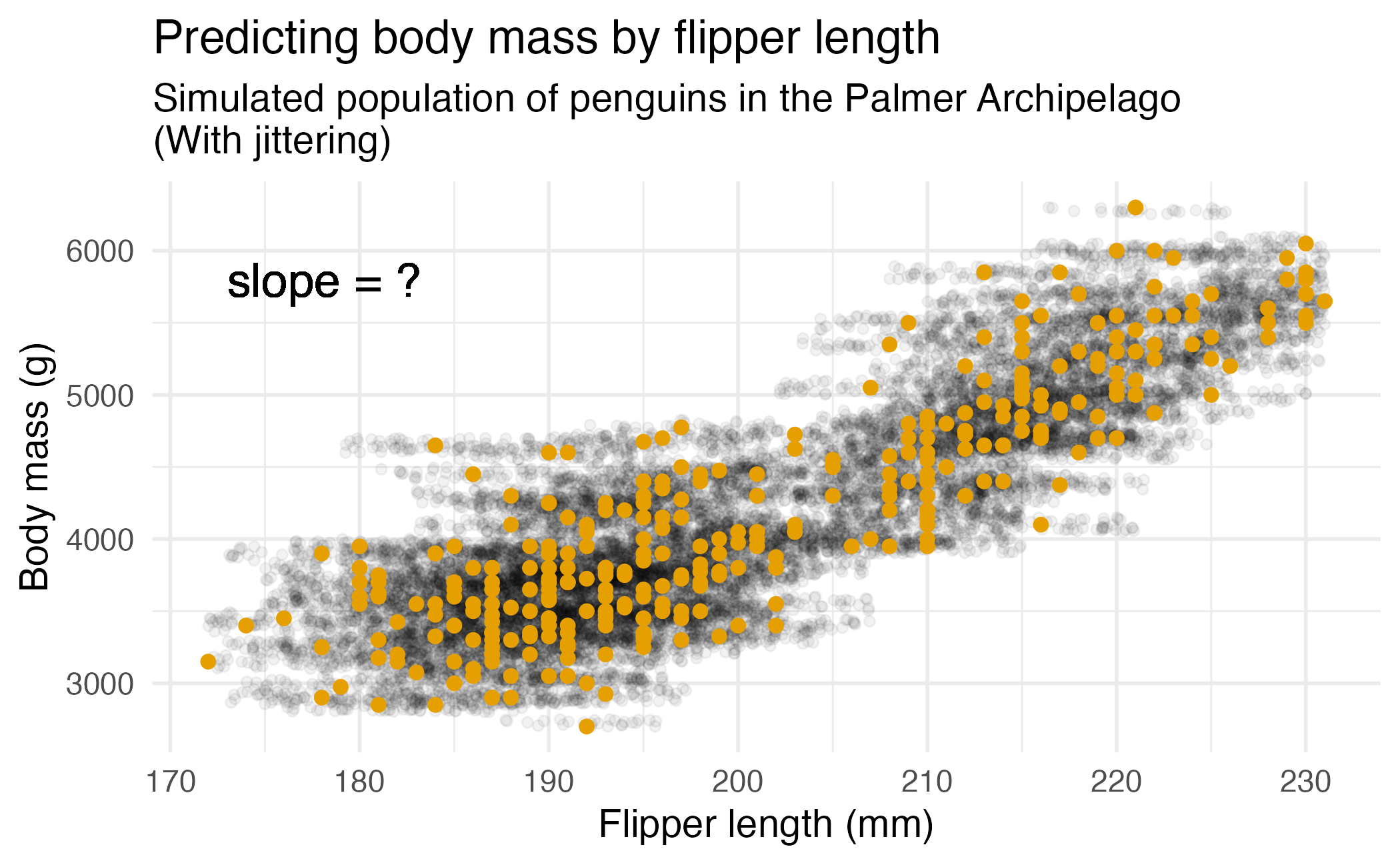
Observed sample
Bootstrap population
Generated assuming there are more penguins like the ones in the observed sample…

Random sampling
Random sampling
Sampling without replacement
Sampling with replacement
Random sampling
Sample without replacement
[1] 8 4 2 3 5 1 6 9 7 10 [1] 3 7 1 2 4 9 6 5 8 10 [1] 8 6 7 10 5 9 3 1 2 4Bootstrapping scheme
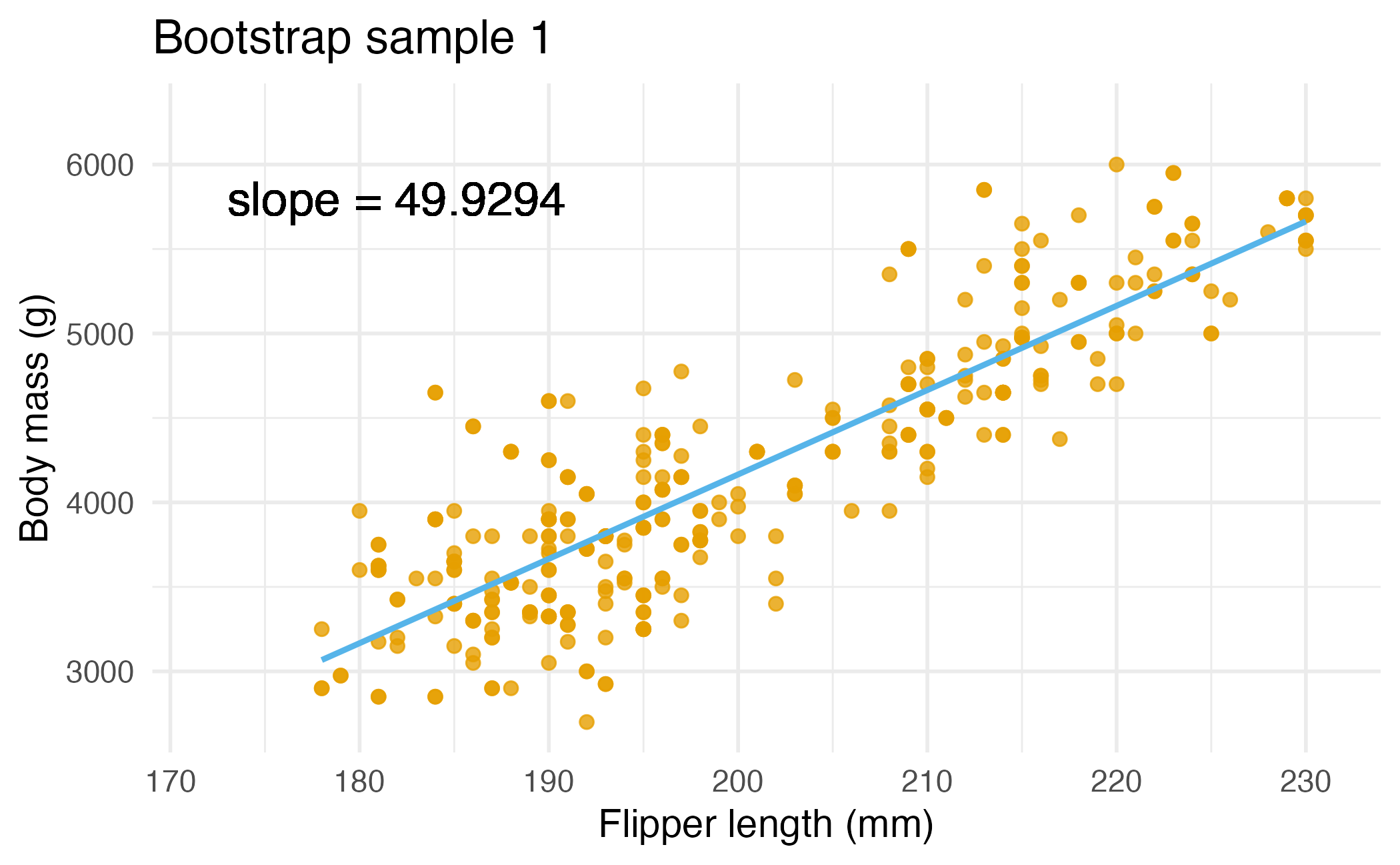
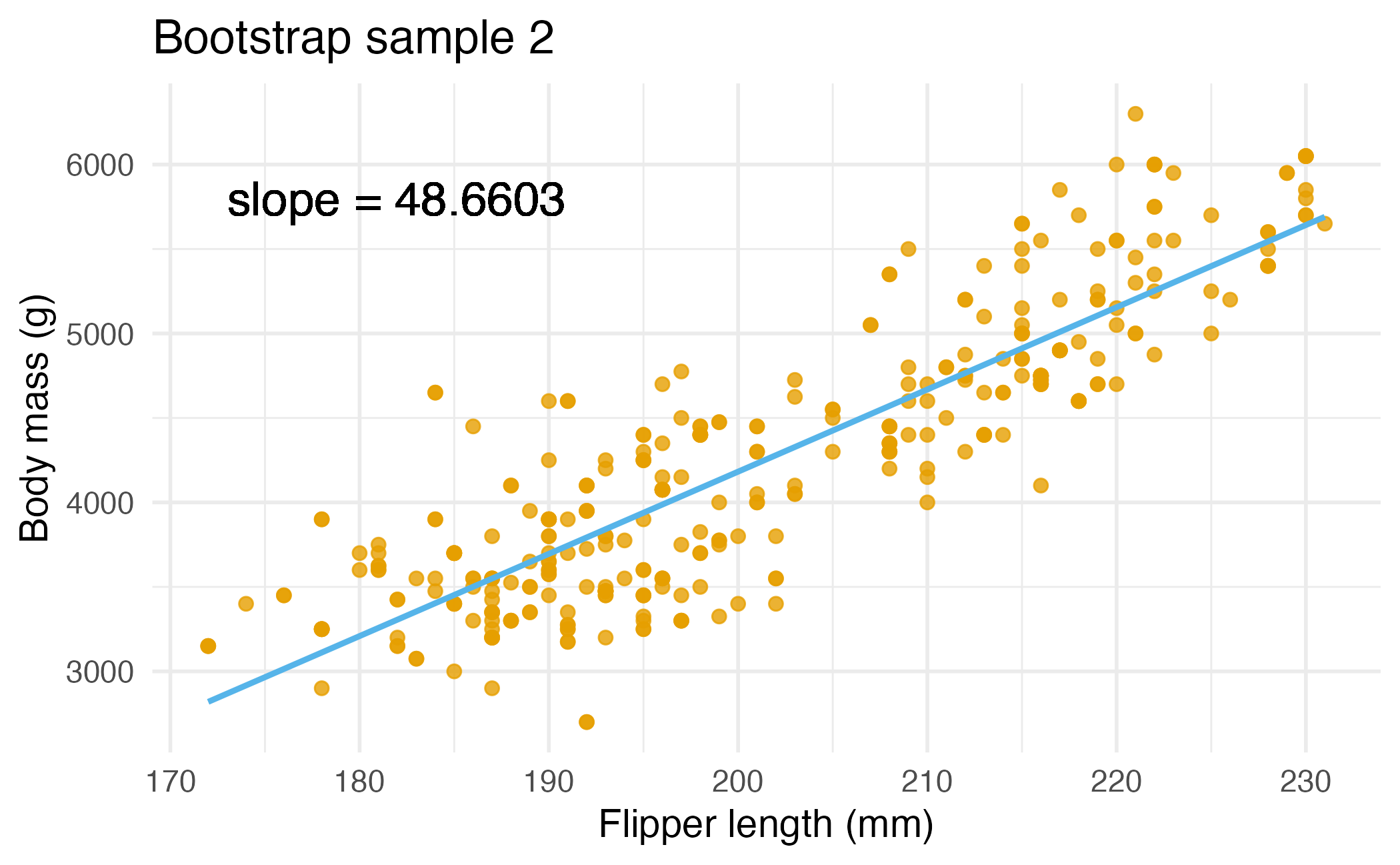
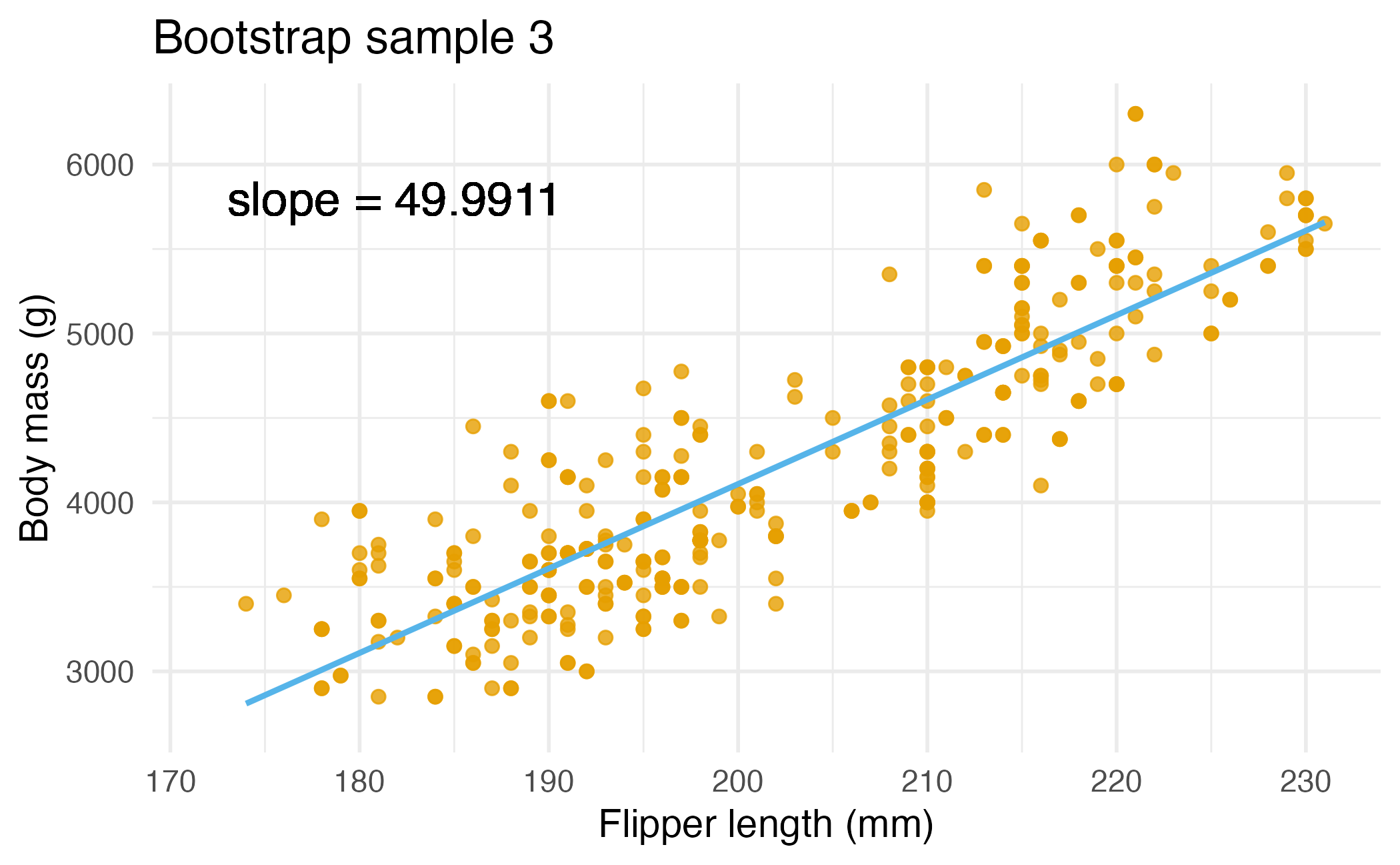
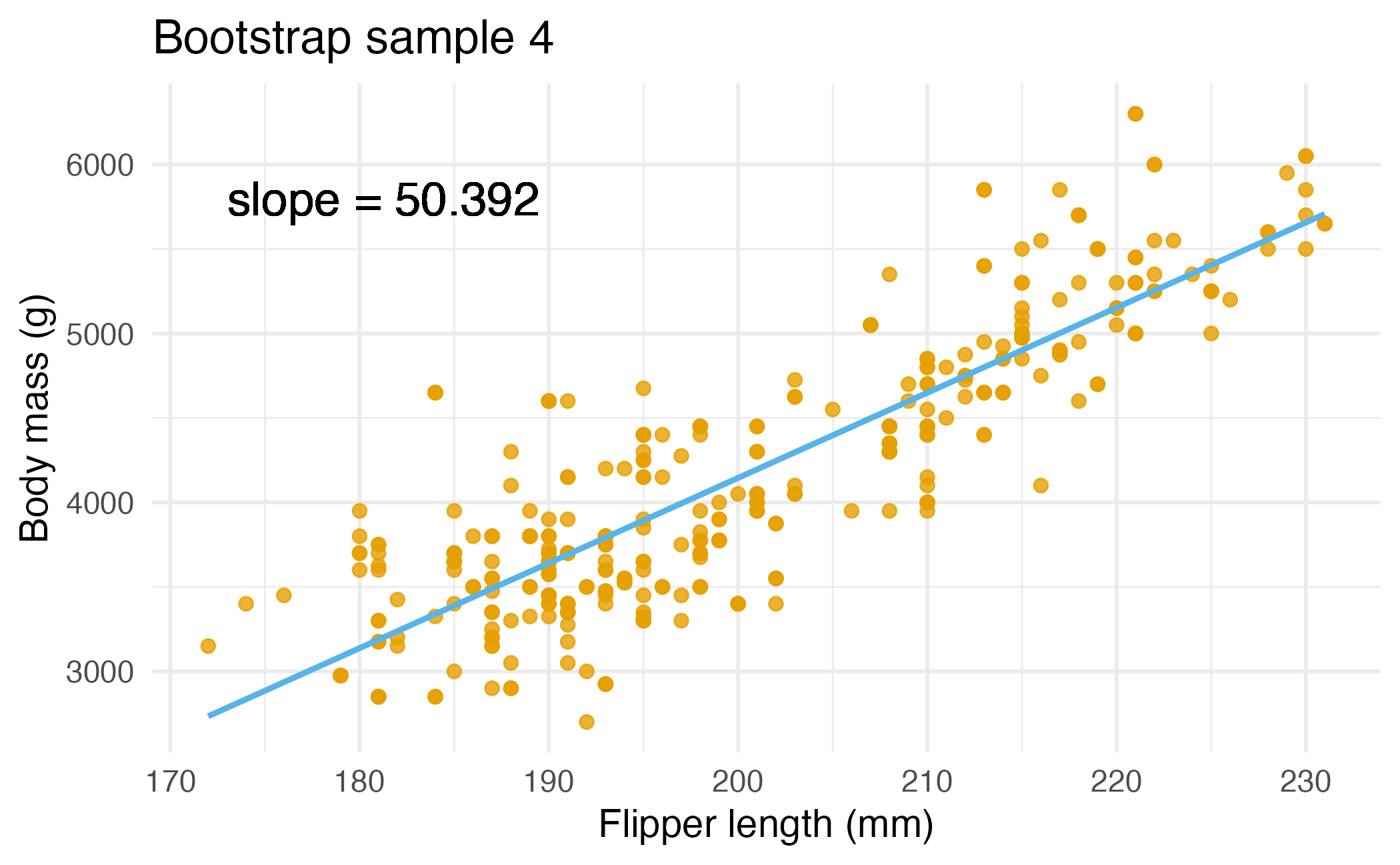
- Take a bootstrap sample - a random sample taken with replacement from the original sample, of the same size as the original sample
- Calculate the bootstrap statistic - a statistic such as mean, median, proportion, slope, etc. computed on the bootstrap samples
- Repeat steps (1) and (2) many times to create a bootstrap distribution - a distribution of bootstrap statistics
- Calculate the bounds of the XX% confidence interval as the middle XX% of the bootstrap distribution
Bootstrap sample 1
Bootstrap sample 2
Bootstrap sample 3
Bootstrap sample 4
Bootstrap samples 1 - 4
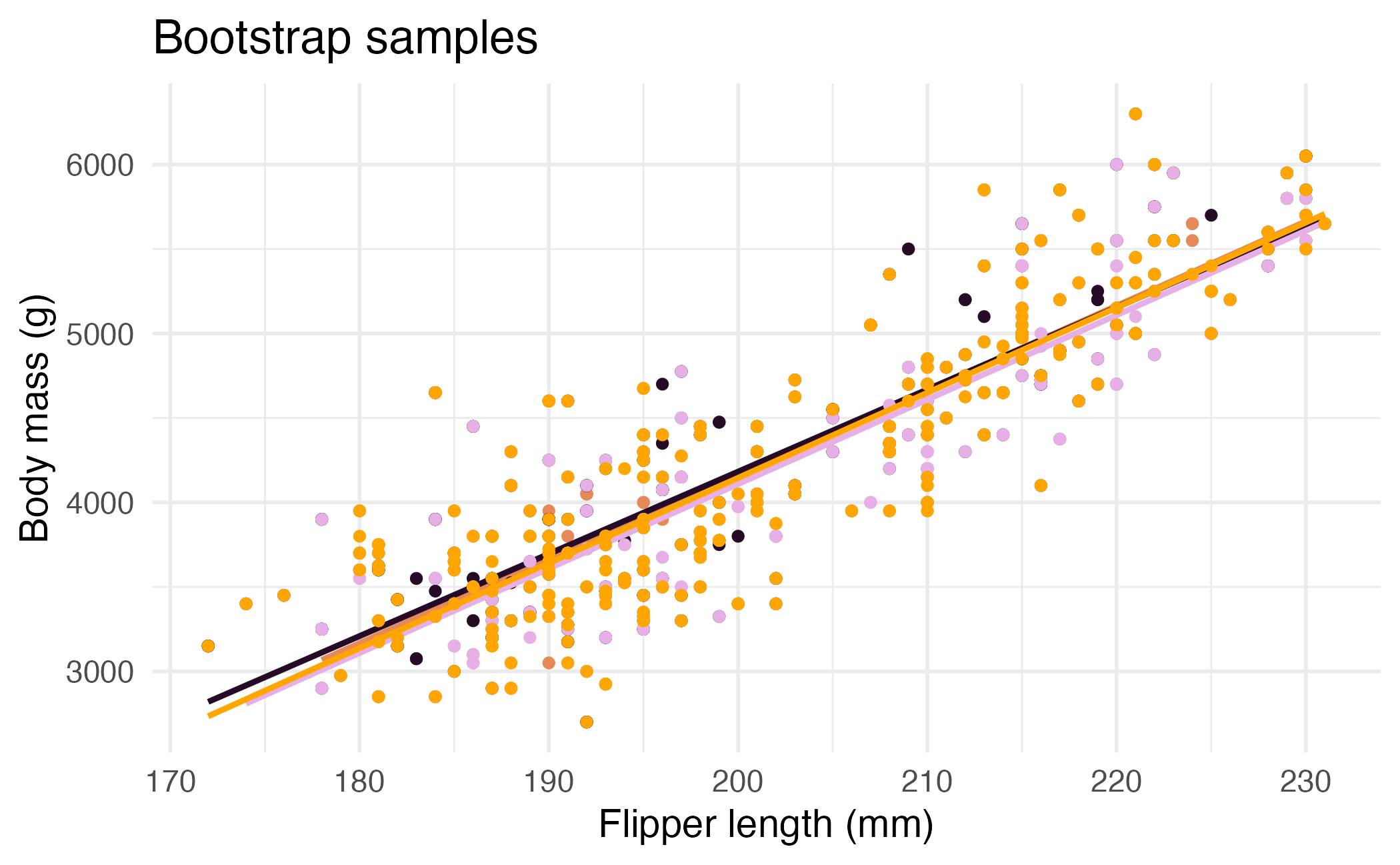
we could keep going…
Many many samples…
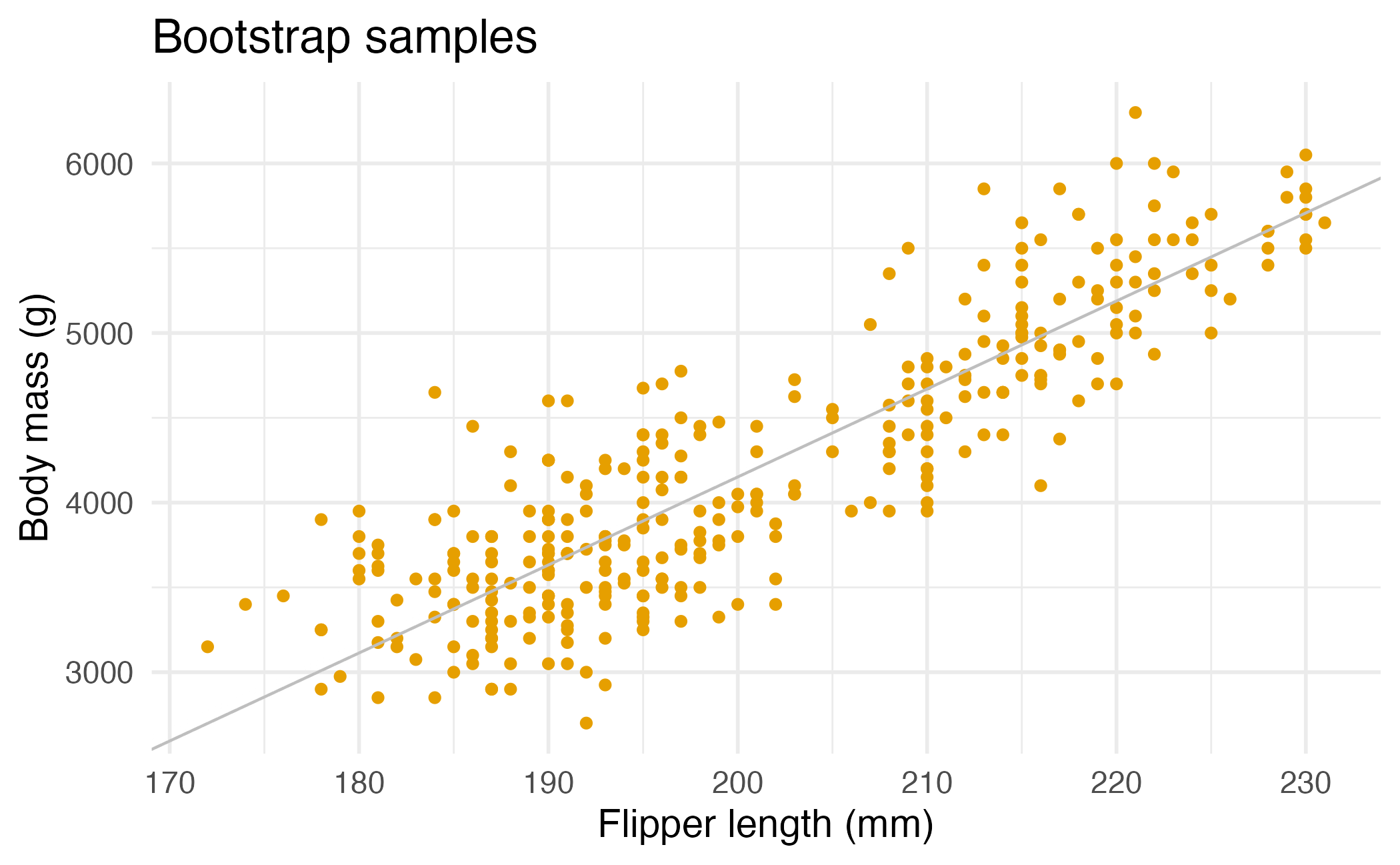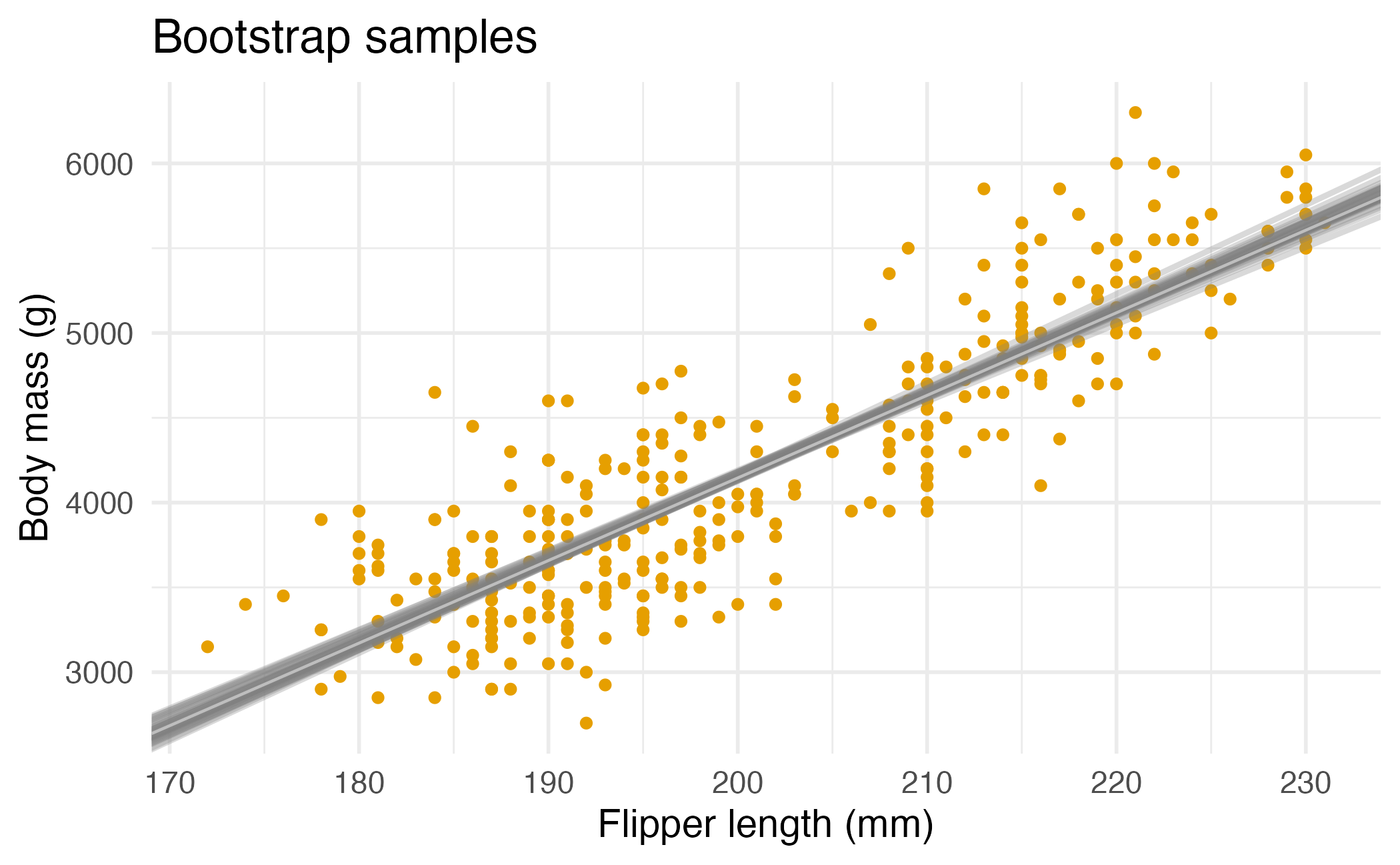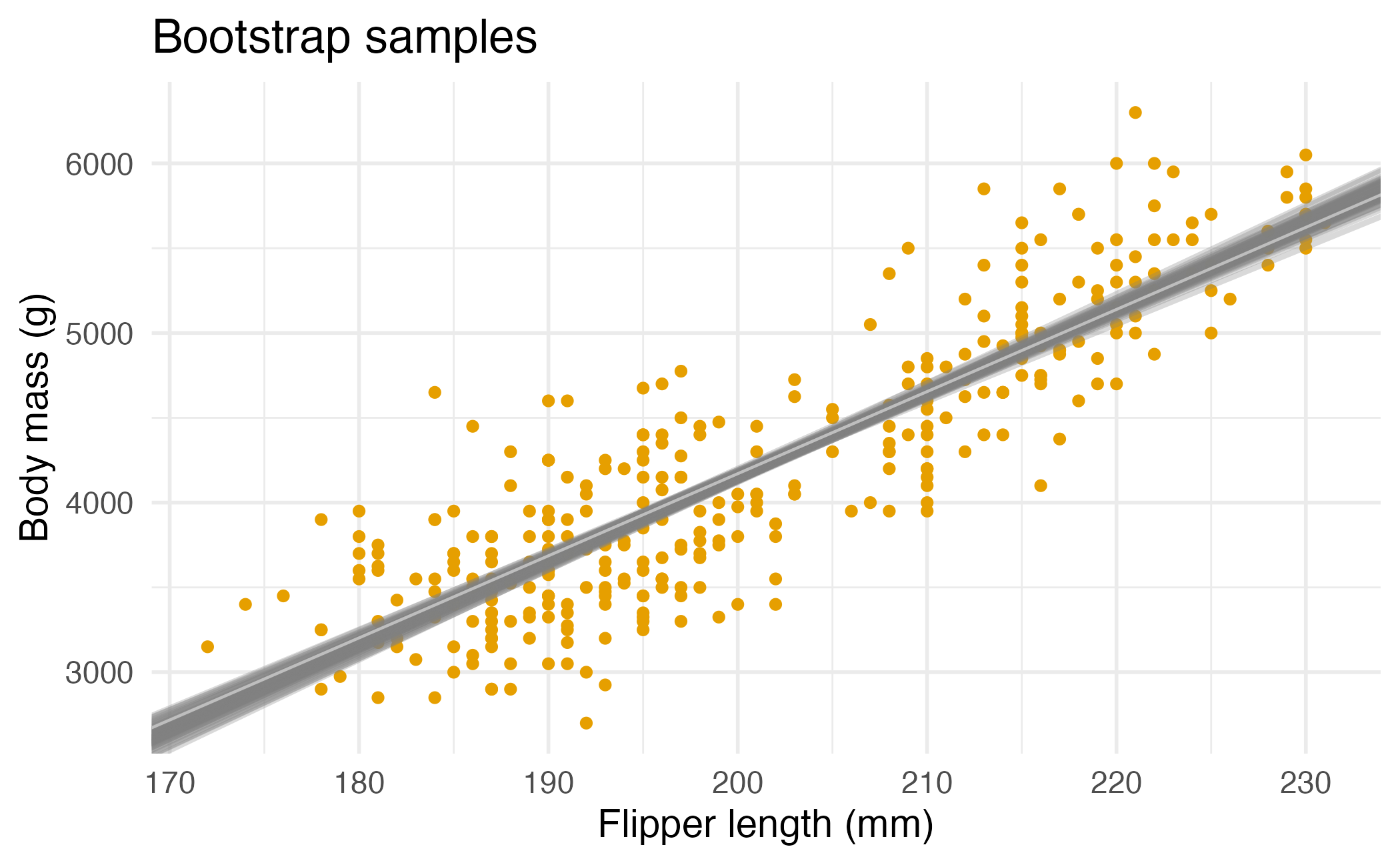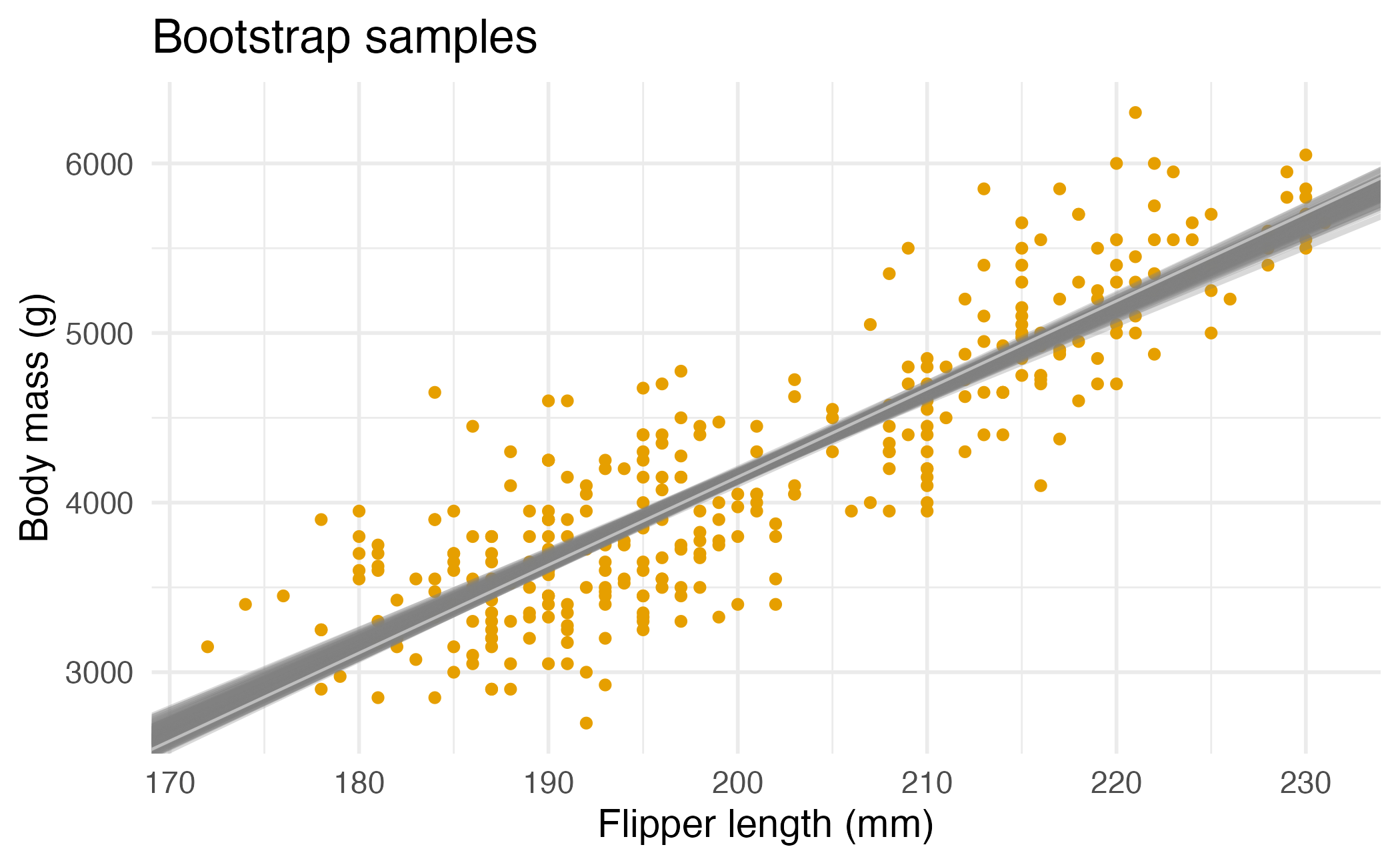
Slopes of bootstrap samples
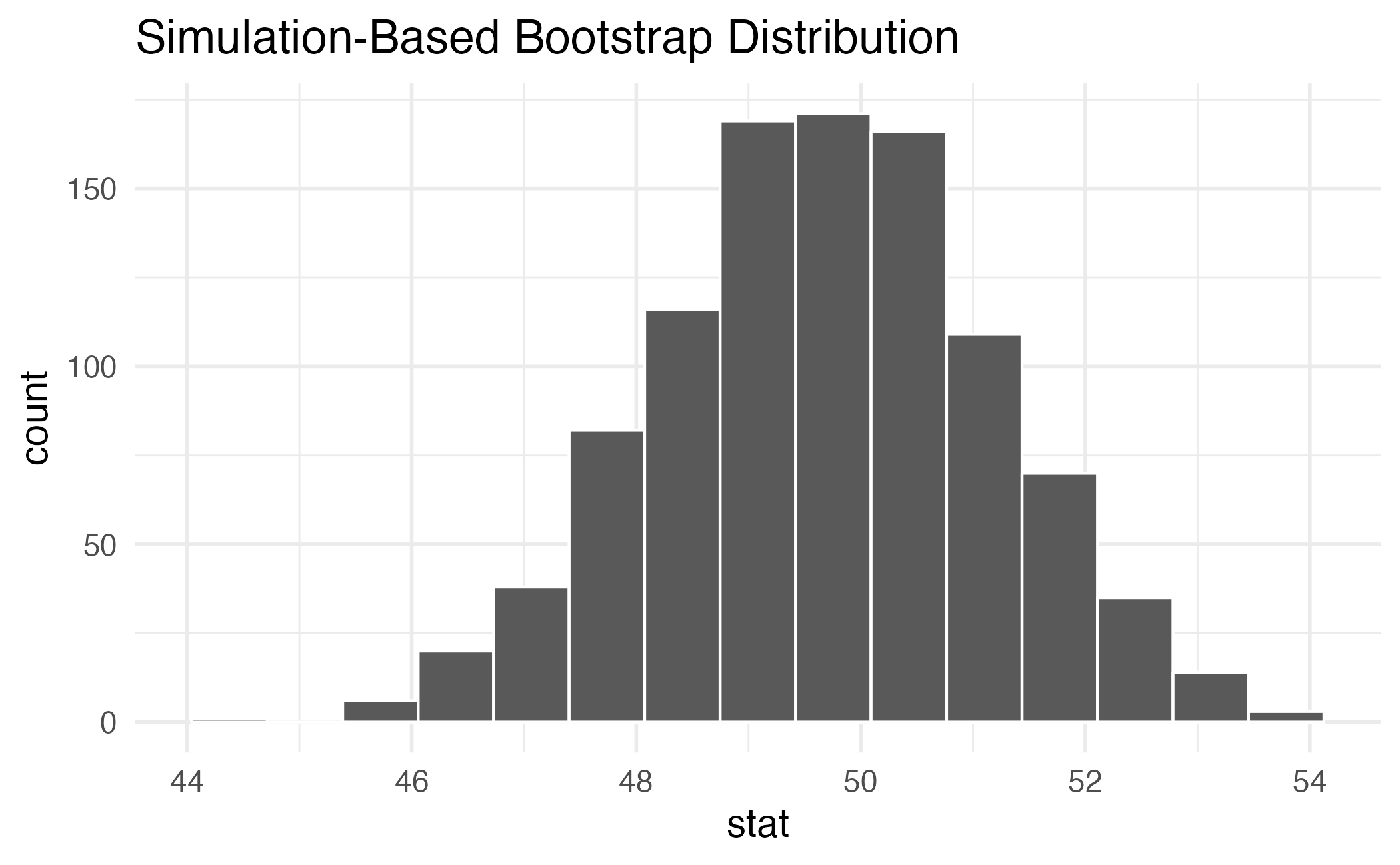
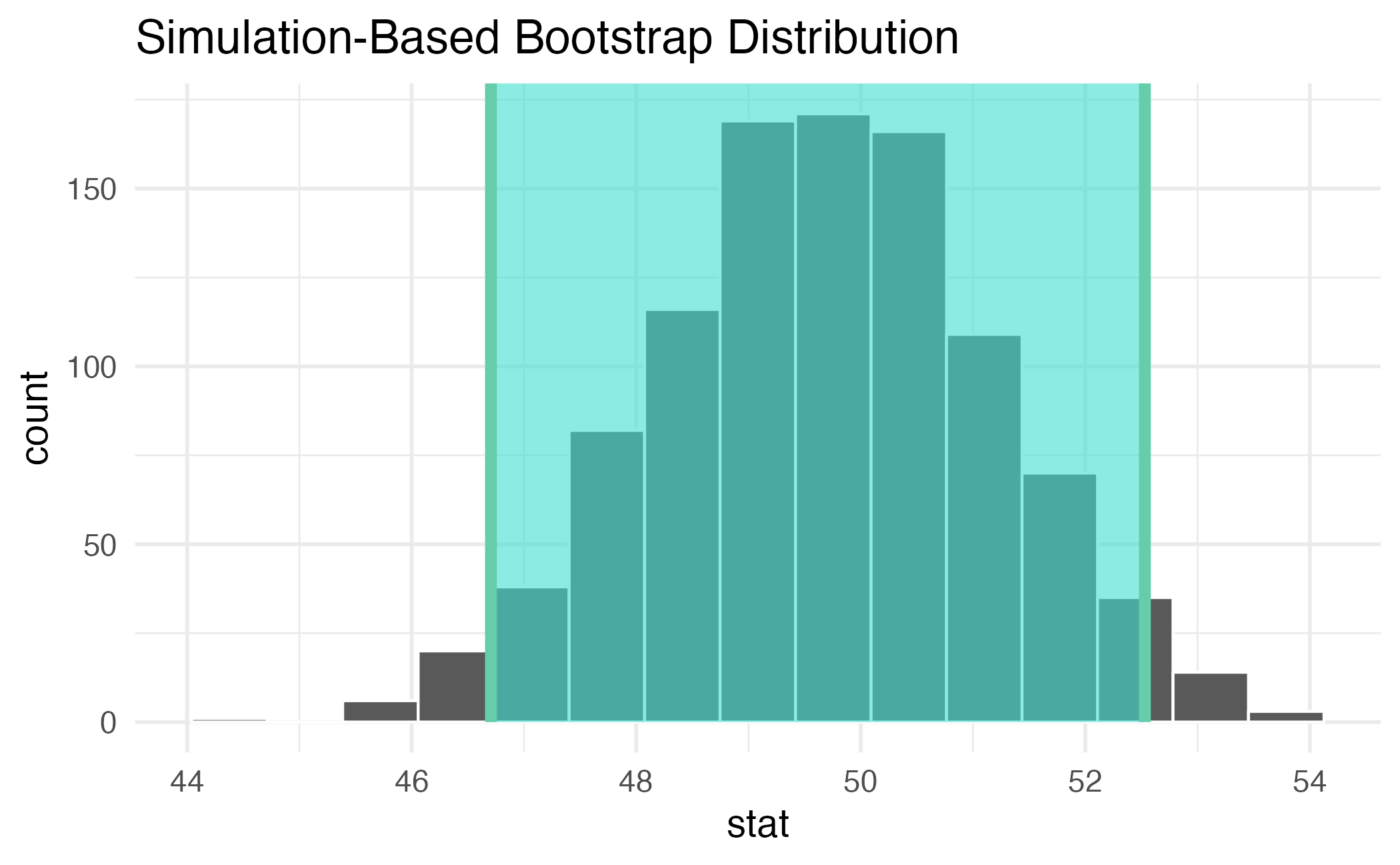
95% confidence interval
Interpreting the slope, take two
# A tibble: 1 × 2
lower_ci upper_ci
<dbl> <dbl>
1 46.7 52.5We are 95% confident that for each additional millimeter of flipper length, we would expect penguins to have a body mass 46.71 to 52.53 grams higher, on average.
Some notes on confidence intervals
Confidence level
We are 95% confident that …
- Suppose we took many samples from the original population and built a 95% confidence interval based on each sample.
- Then about 95% of those intervals would contain the true population parameter.
Confidence intervals identify a plausible range of values for the population parameter…
…they do not identify the probability that the true population parameter falls within the specified range.

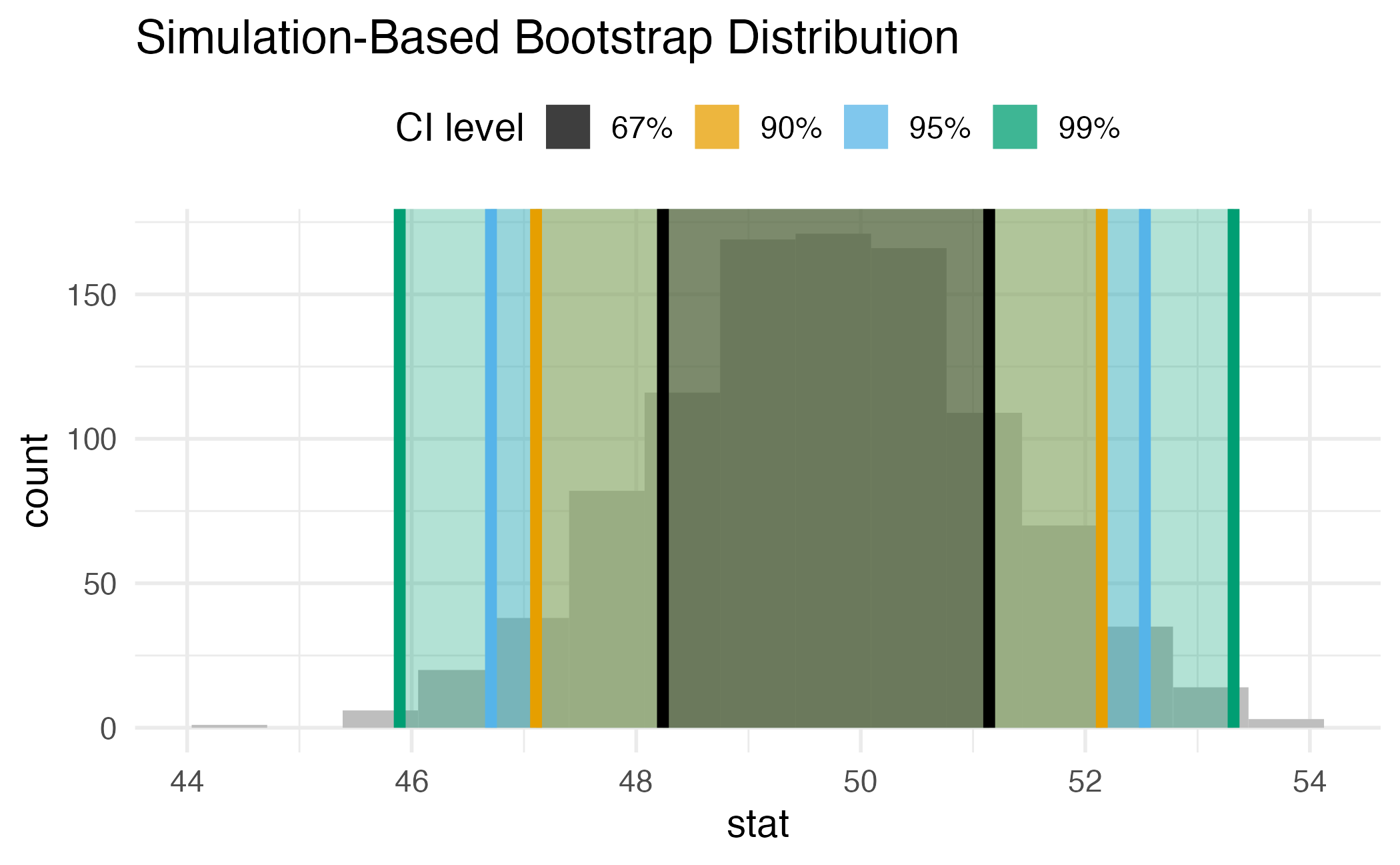
Commonly used confidence intervals
Precision vs. accuracy
If we want to be very certain that we capture the population parameter, should we use a wider or a narrower interval? What drawbacks are associated with using a wider interval?

How can we get best of both worlds – high precision and high accuracy?
Connection between hypothesis testing and confidence intervals
Confidence intervals vs. hypothesis testing
Related, but have distinct motivations
- Estimation \(\leadsto\) confidence interval
- Decision \(\leadsto\) hypothesis test
Confidence interval vs. \(p\)-value
Confidence interval: range of plausible values for the population parameter
Distribution centered around the observed sample statistic
\(p\)-value: probability of observing the data, given the null hypothesis is true
Distribution centered around the value from the null hypothesis
XX% confidence interval is equivalent to hypothesis test at \(\alpha = 1 - XX\%\)
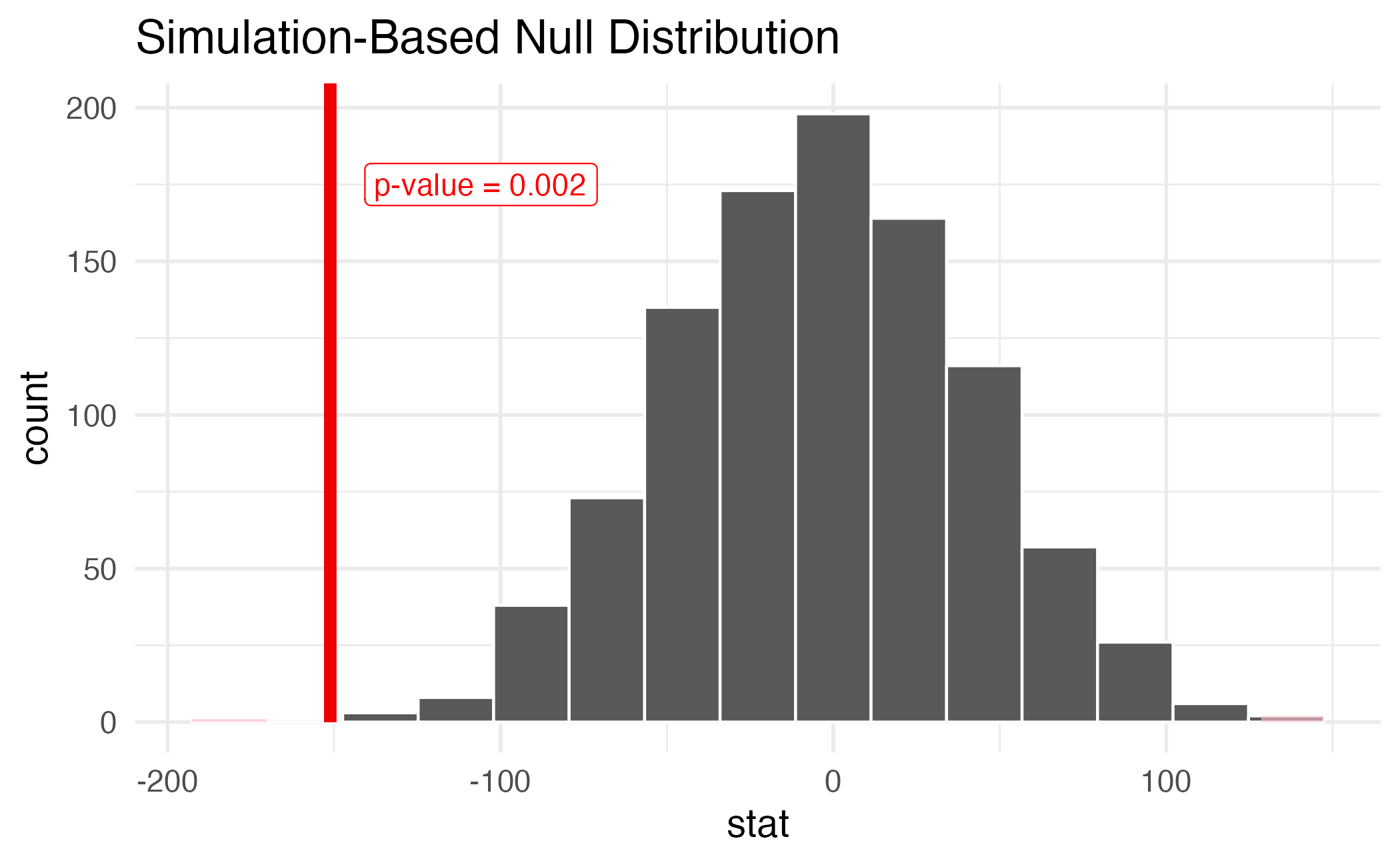
Confidence interval vs. \(p\)-value
Null hypothesis: The typical penguin has a body mass of 4100 grams.
\[H_0: \mu = 4100\]
Alternative hypothesis: The typical penguin has a body mass different than 4100 grams.
\[H_A: \mu \neq 4100\]
Hypothesis test
# A tibble: 1 × 1
p_value
<dbl>
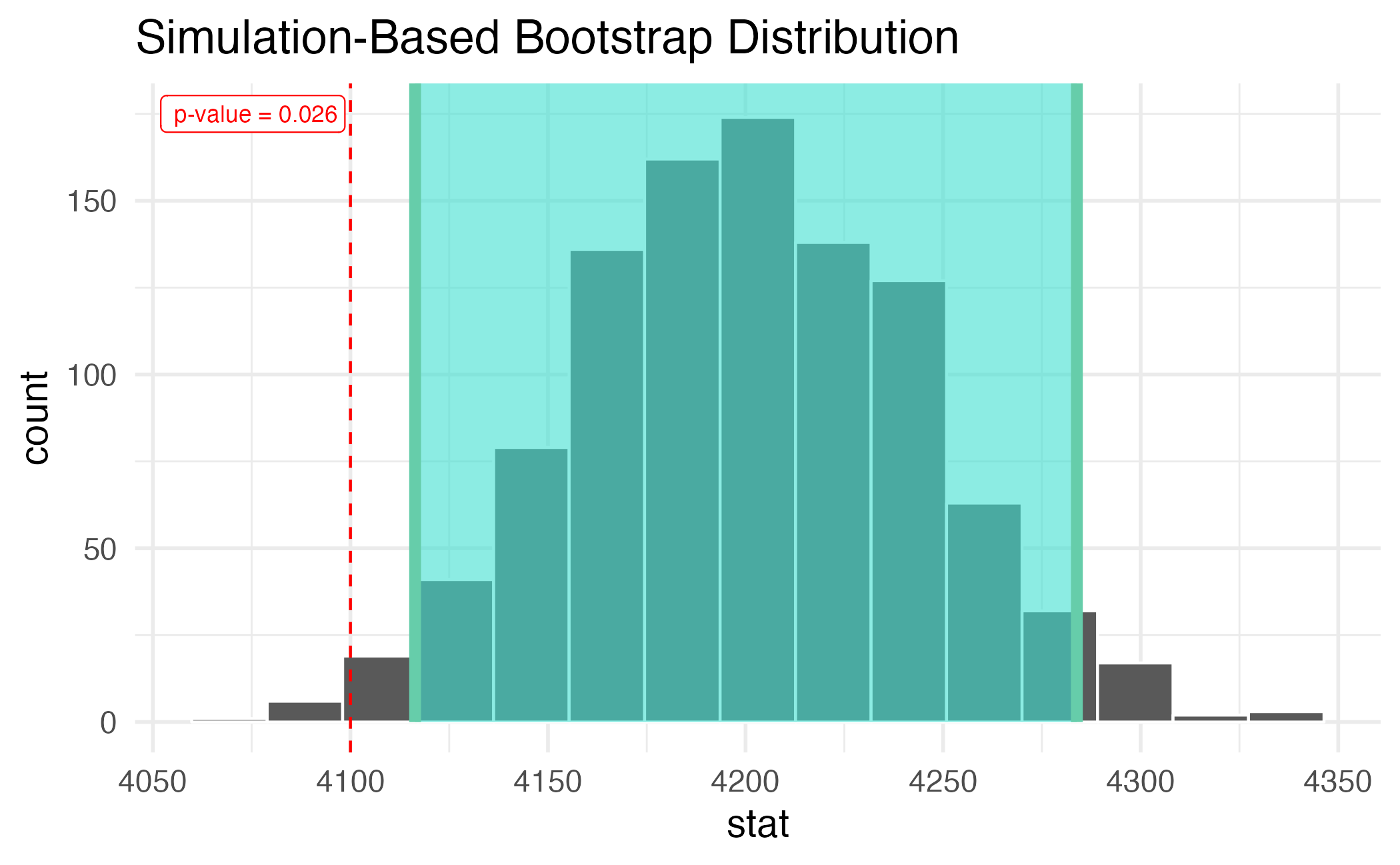
1 0.026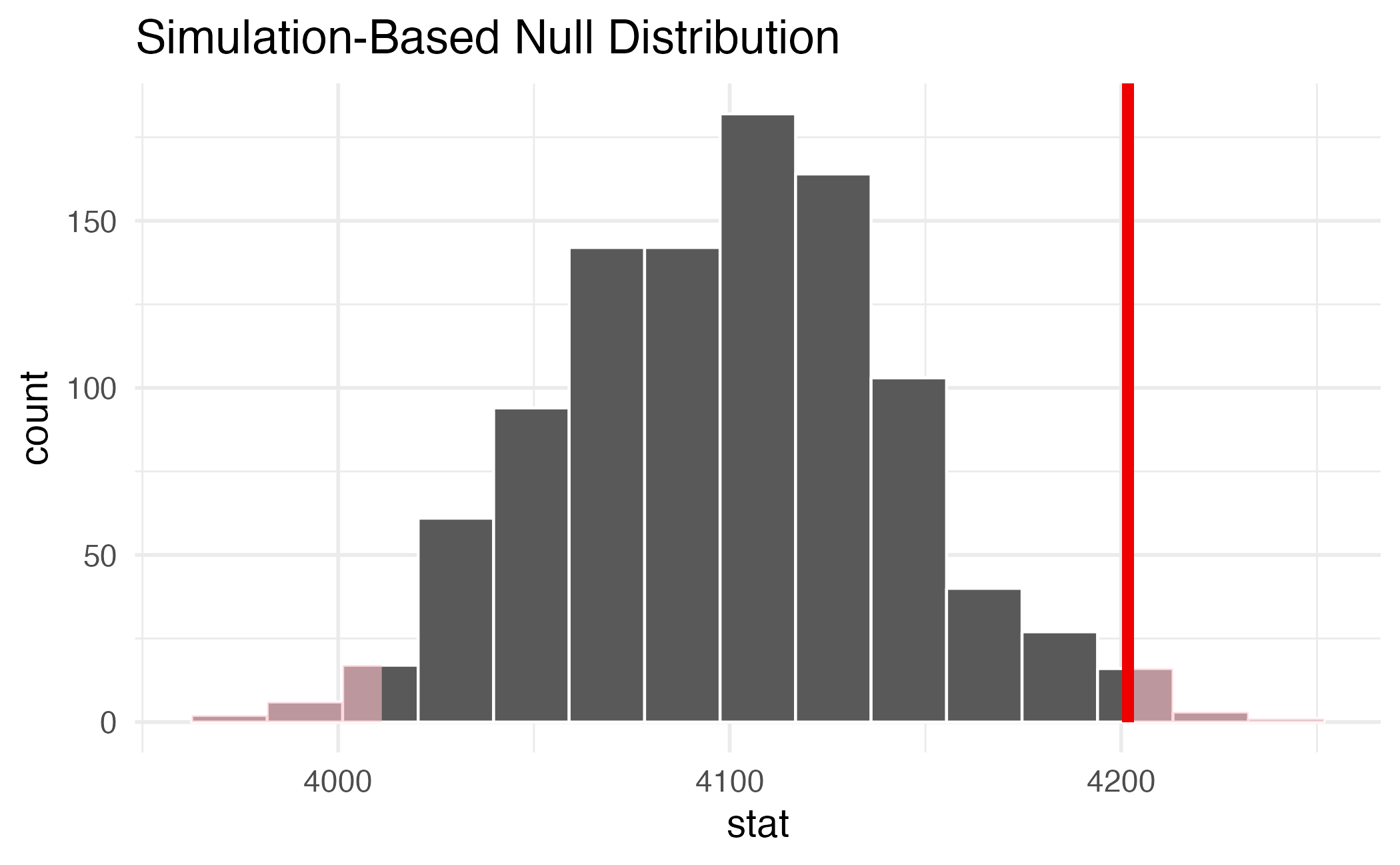
95% confidence interval
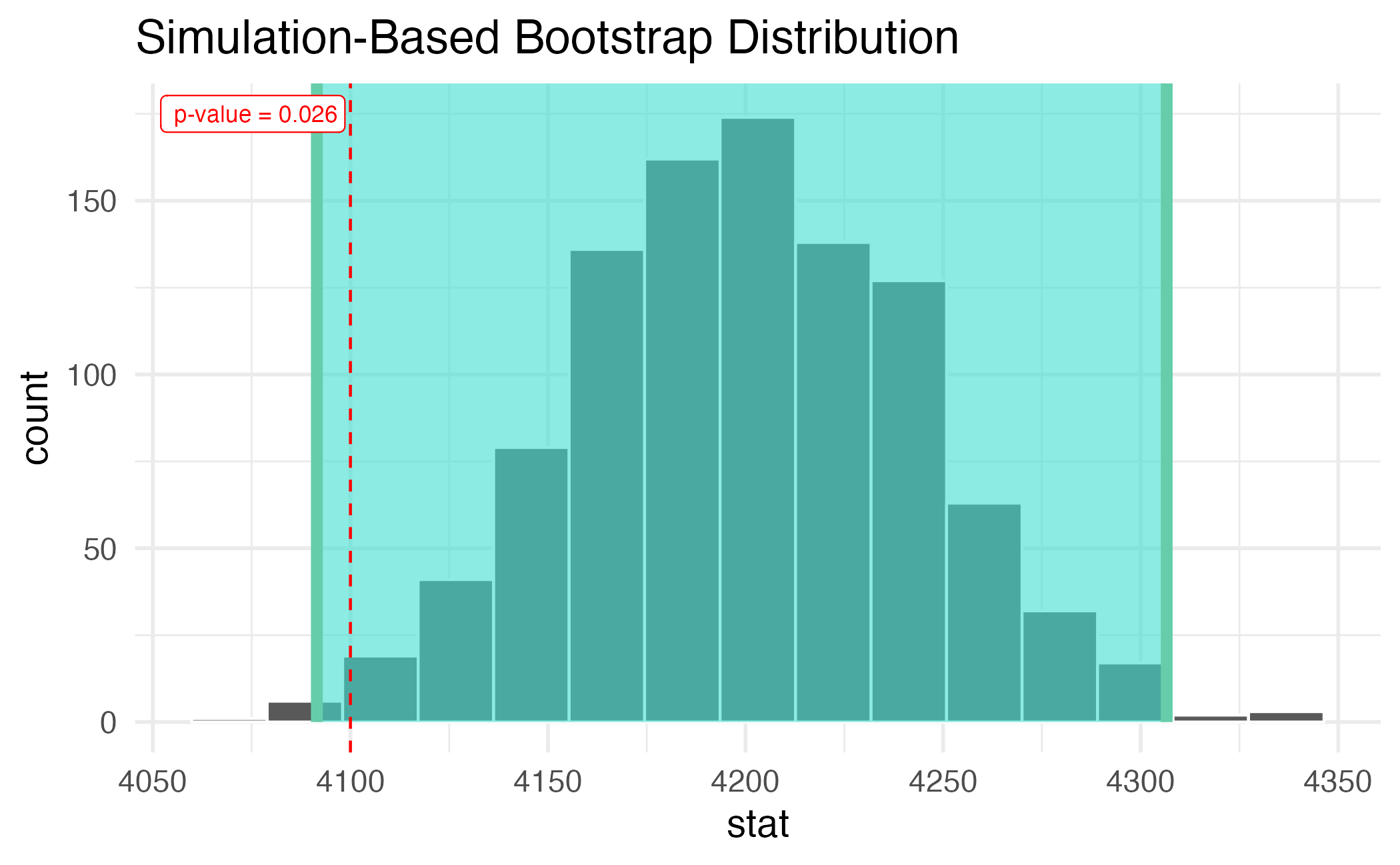
99% confidence interval
Application exercise
Math (and unit conversion) is hard
Corrected null hypothesis test
ae-19
- Go to the course GitHub org and find your
ae-19(repo name will be suffixed with your GitHub name). - Clone the repo in RStudio Workbench, open the Quarto document in the repo, and follow along and complete the exercises.
- Save, commit, and push your edits by the AE deadline – end of the day tomorrow.
Recap of AE
- Sample statistic \(\ne\) population parameter, but if the sample is good, it can be a good estimate
- We report the estimate with a confidence interval, and the width of this interval depends on the variability of sample statistics from different samples from the population
- Since we can’t continue sampling from the population, we bootstrap from the one sample we have to estimate sampling variability
- We can do this for any sample statistic:
- For a mean:
calculate(stat = "mean") - For a median:
calculate(stat = "median") - For a regression model:
fit() - Full infer pipeline examples
- For a mean:
Acknowledgments
- Draws upon material from Data Science in a Box licensed under Creative Commons Attribution-ShareAlike 4.0 International
Bought a car
