library(tidyverse)
library(scales)AE 02: Visualizing the prognosticators
Suggested answers
These are suggested answers. This document should be used as reference only, it’s not designed to be an exhaustive key.
Below are the contents of the YAML header. You normally do not see this in the rendered file - we include it so you can reproduce the figure dimensions in the document.
---
title: "AE 02: Visualizing the prognosticators"
subtitle: "Suggested answers"
execute:
fig-width: 8
fig-height: 4
warning: false
---For all analyses, we’ll use the tidyverse packages.
Data: The prognosticators
The dataset we will visualize is called seers.1 It contains summary statistics for all known Groundhog Day forecasters. 2 Let’s glimpse() at it .
# import data using readr::read_csv()
seers <- read_csv("data/prognosticators-sum-stats.csv")
glimpse(seers)Rows: 138
Columns: 18
$ name <chr> "Allen McButterpants", "Arboretum Annie", "Beard…
$ forecaster_type <chr> "Groundhog", "Groundhog", "Stuffed Prairie Dog",…
$ forecaster_simple <chr> "Groundhog", "Groundhog", "Other", "Other", "Oth…
$ alive <lgl> TRUE, TRUE, FALSE, TRUE, TRUE, TRUE, TRUE, TRUE,…
$ climate_region <chr> "Northeast", "South", "Northeast", "South", "Ohi…
$ town <chr> "Hampton Bays", "Dallas", "Bridgeport", "Bee Cav…
$ state <chr> "NY", "TX", "CT", "TX", "OH", "TX", "TX", "AL", …
$ preds_n <dbl> 1, 3, 12, 13, 8, 7, 1, 1, 12, 2, 4, 13, 10, 1, 4…
$ preds_long_winter <dbl> 0, 1, 1, 3, 4, 5, 1, 1, 6, 2, 2, 8, 9, 0, 12, 6,…
$ preds_long_winter_pct <dbl> 0.00000000, 0.33333333, 0.08333333, 0.23076923, …
$ preds_correct <dbl> 1, 2, 9, 9, 5, 3, 0, 0, 5, 0, 2, 5, 2, 0, 23, 0,…
$ preds_rate <dbl> 1.0000000, 0.6666667, 0.7500000, 0.6923077, 0.62…
$ temp_mean <dbl> 32.40000, 50.18333, 31.13333, 51.30769, 40.29375…
$ temp_hist <dbl> 30.14667, 51.32000, 29.56639, 50.97615, 38.88542…
$ temp_sd <dbl> 4.120782, 3.890902, 4.120782, 3.890902, 4.706475…
$ precip_mean <dbl> 2.395000, 2.768333, 3.012500, 2.593462, 4.088125…
$ precip_hist <dbl> 2.9743333, 2.5588889, 3.0695000, 2.5643846, 3.37…
$ precip_sd <dbl> 0.9620579, 0.9029786, 0.9620579, 0.9029786, 1.18…The variables are:
name- name of the prognosticatorforecaster_type- what kind of animal or thing is the prognosticator?forecaster_simple- a simplified version that lumps together the least-frequently appearing types of prognosticatorsalive- is the prognosticator an animate (alive) being?3climate_region- the NOAA climate region in which the prognosticator is located.town- self-explanatorystate- state (or territory) where prognosticator is locatedpreds_n- number of predictions in the databasepreds_long_winter- number of predictions for a “Late Winter” (as opposed to “Early Spring”)preds_long_winter_pct- percentage of predictions for a “Late Winter”preds_correct- number of correct predictions4preds_rate- proportion of predictions that are correcttemp_mean- average temperature (in Fahrenheit) in February and March in the climate region across all prognostication yearstemp_hist- average of the rolling 15-year historic average temperature in February and March across all prognostication yearstemp_sd- standard deviation of average February and March temperatures across all prognostication yearsprecip_mean- average amount of precipitation in February and March across all prognostication years (measured in rainfall inches)precip_histaverage of the rolling 15-year historic average precipitation in February and March across all prognostication yearsprecip_sd- standard deviation of average February and March precipitation across all prognostication years
Visualizing prediction success rate - Demo
Single variable
Analyzing the a single variable is called univariate analysis.
Create visualizations of the distribution of preds_rate for the prognosticators.
- Make a histogram. Set an appropriate binwidth.
Two variables - Your turn
Analyzing the relationship between two variables is called bivariate analysis.
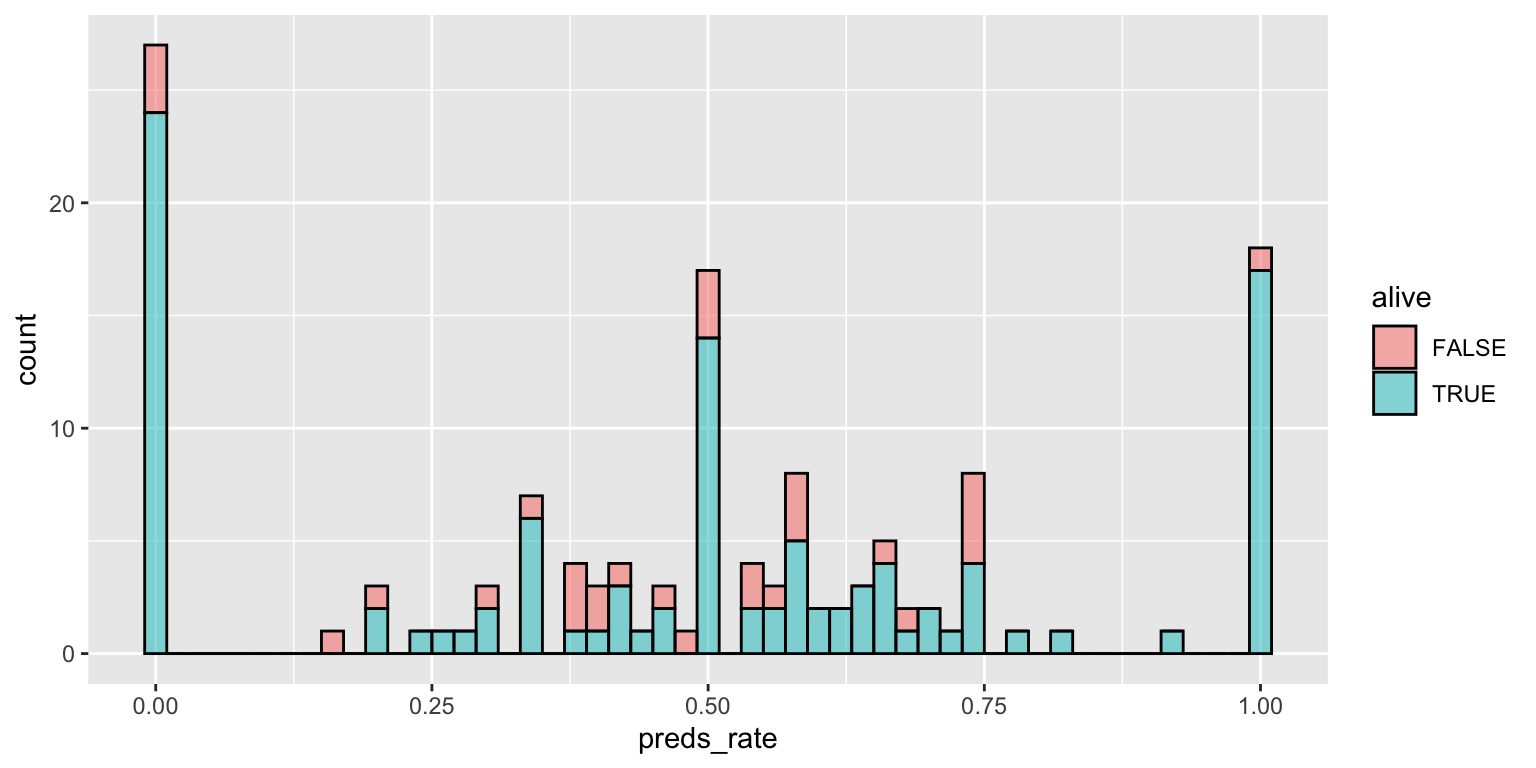
Create visualizations of the distribution of preds_rate by alive (whether or not the prognosticator is alive).
- Make a single histogram. Set an appropriate binwidth.
ggplot(
data = seers,
mapping = aes(x = preds_rate, fill = alive)
) +
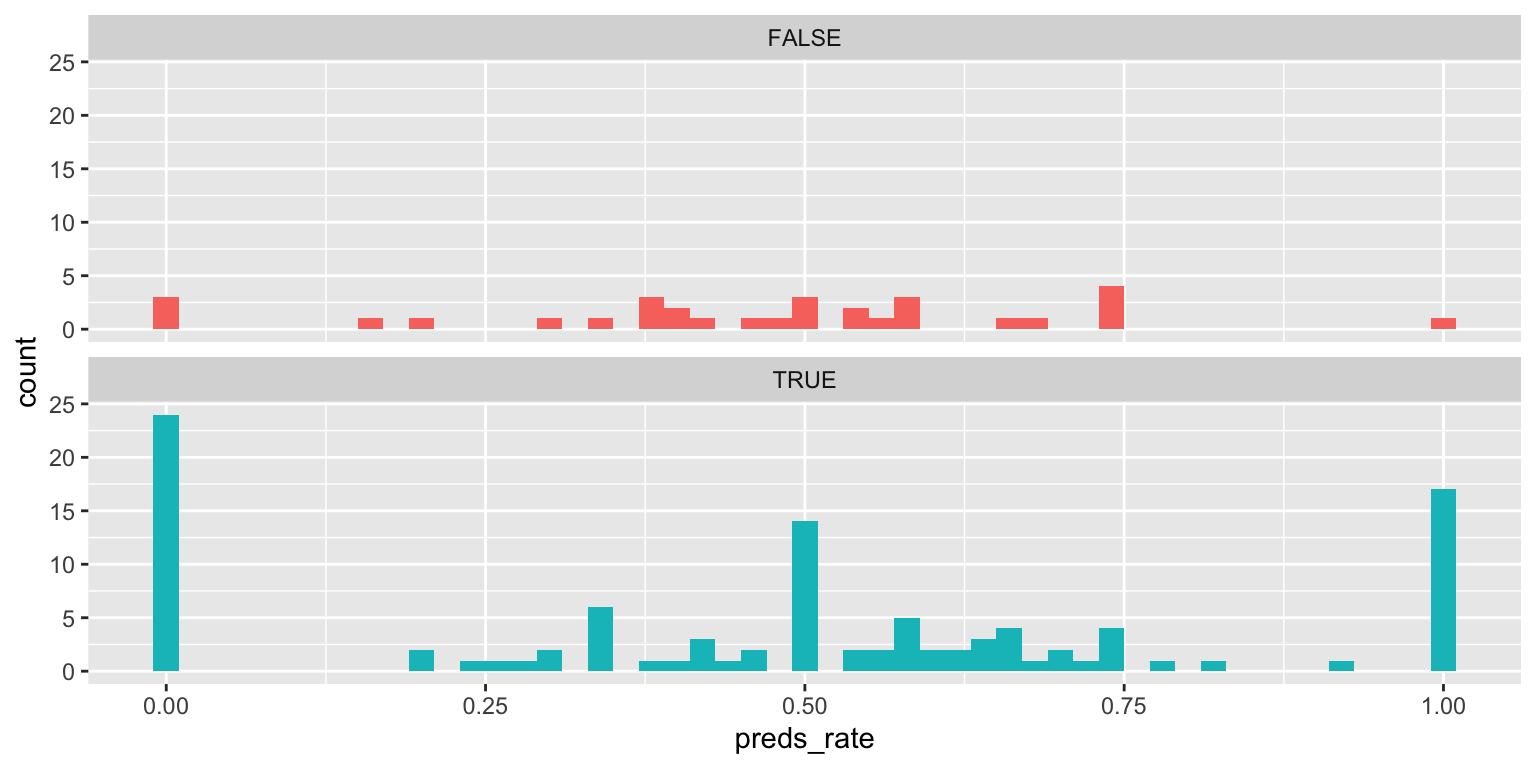
geom_histogram(binwidth = 0.02, alpha = 0.5, color = "black")- Use multiple histograms via faceting, one for each type. Set an appropriate binwidth, add color as you see fit, and turn off legends if not needed.
ggplot(
data = seers,
mapping = aes(x = preds_rate, fill = alive)
) +
geom_histogram(binwidth = 0.02, show.legend = FALSE) +
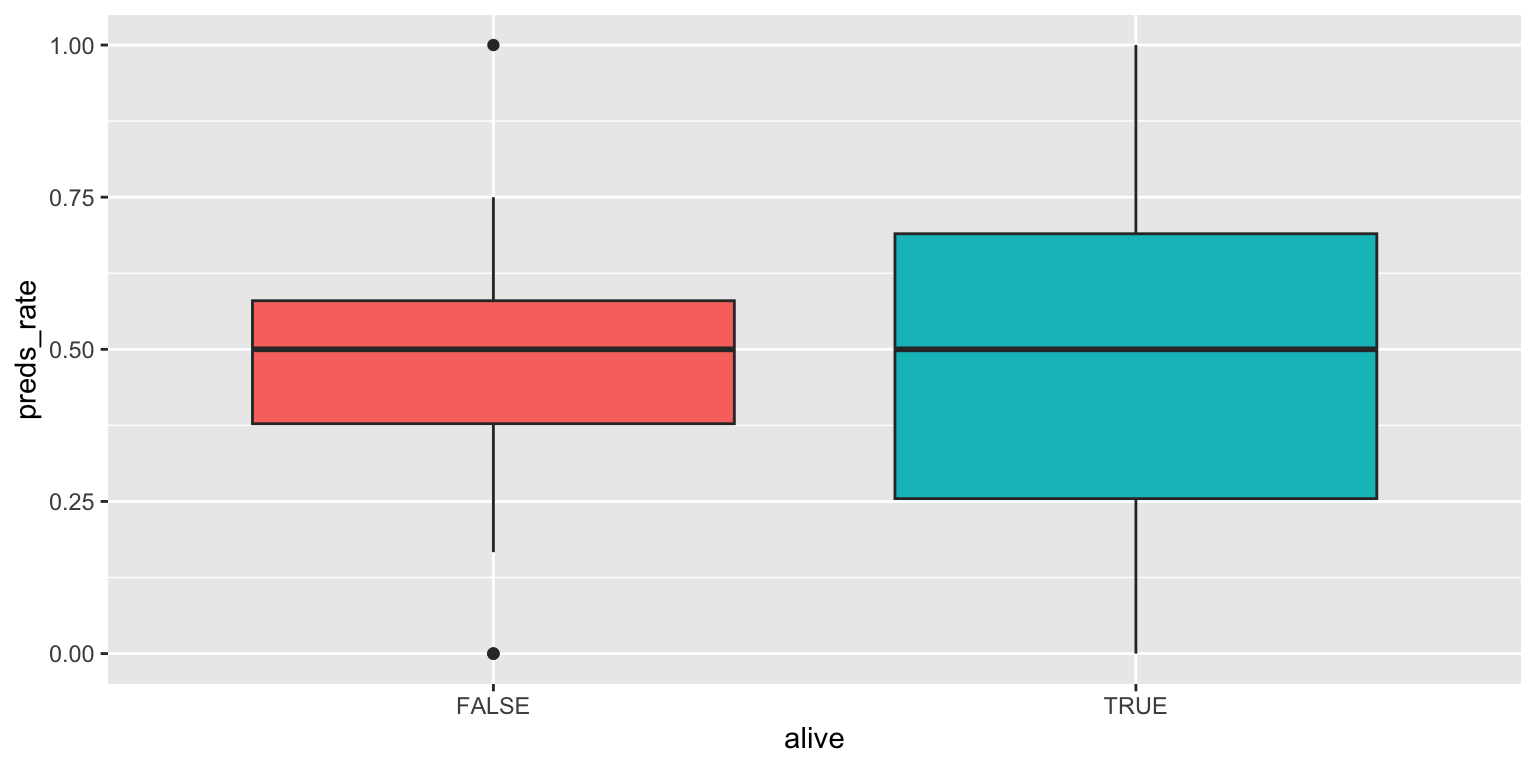
facet_wrap(vars(alive), ncol = 1)- Use side-by-side box plots. Add color as you see fit and turn off legends if not needed.
ggplot(
data = seers,
mapping = aes(x = alive, y = preds_rate, fill = alive)
) +
geom_boxplot(show.legend = FALSE)- Use a density plot. Add color as you see fit.
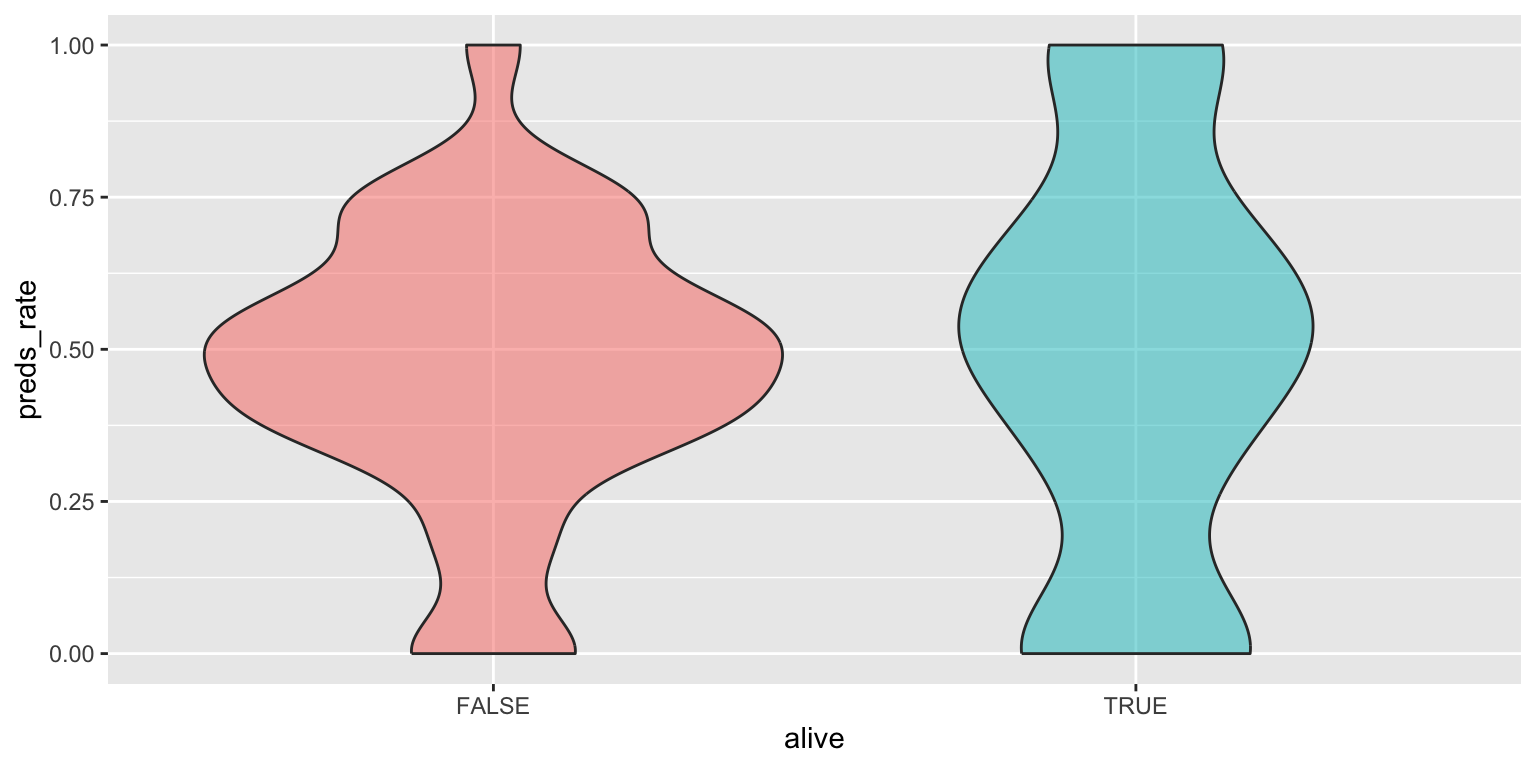
- Use a violin plot. Add color as you see fit and turn off legends if not needed.
ggplot(
data = seers,
mapping = aes(x = alive, y = preds_rate, fill = alive)
) +
geom_violin(alpha = 0.5, show.legend = FALSE)- Make a jittered scatter plot. Add color as you see fit and turn off legends if not needed.
ggplot(
data = seers,
mapping = aes(x = alive, y = preds_rate, color = alive)
) +
geom_jitter(show.legend = FALSE)- Use beeswarm plots. Add color as you see fit and turn off legends if not needed.
library(ggbeeswarm)
ggplot(
data = seers,
mapping = aes(x = alive, y = preds_rate, color = alive)
) +
geom_beeswarm(show.legend = FALSE)- Demonstration: Use multiple geoms on a single plot. Be deliberate about the order of plotting. Change the theme and the color scale of the plot. Finally, add informative labels.
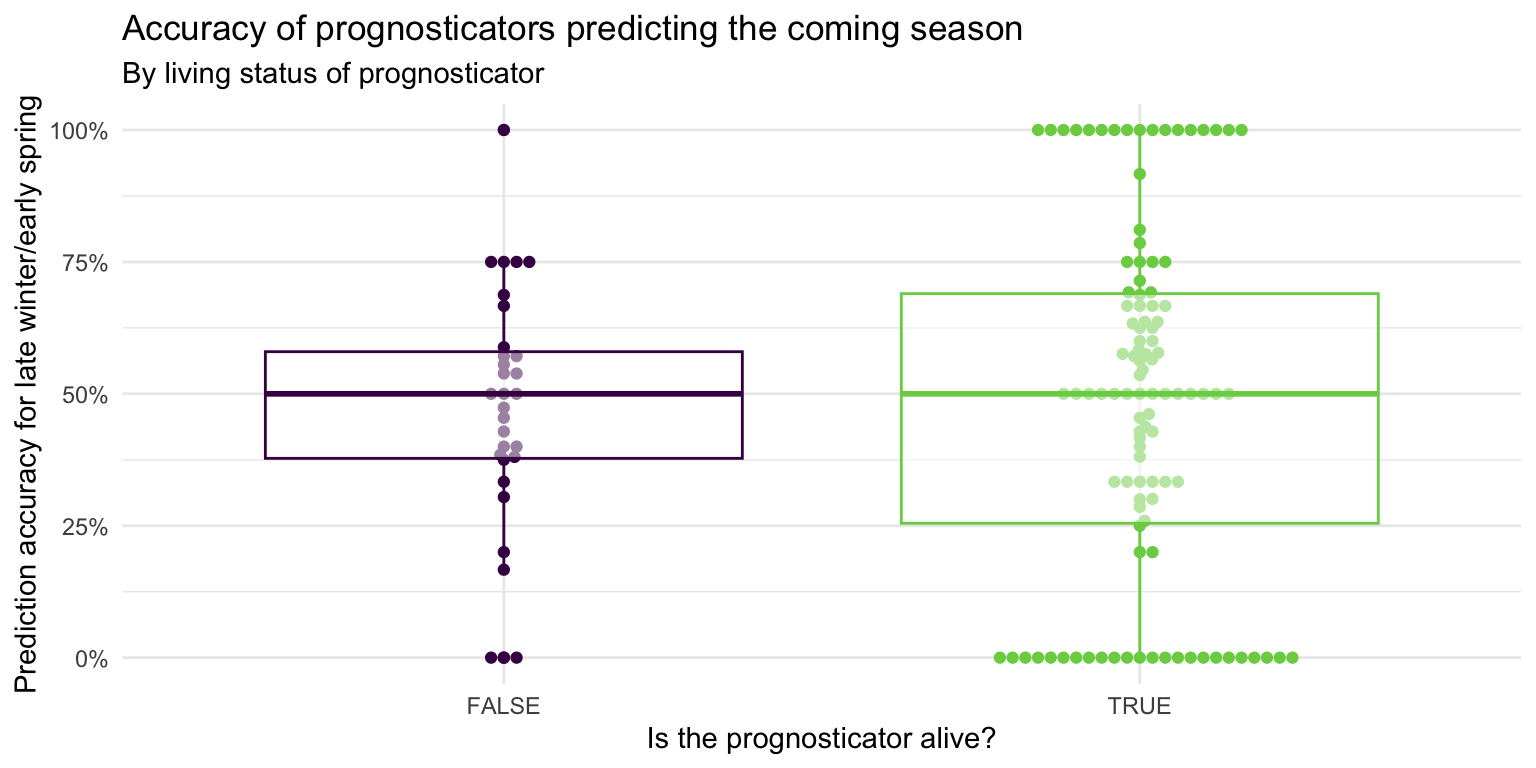
ggplot(
data = seers,
mapping = aes(x = alive, y = preds_rate, color = alive)
) +
geom_beeswarm(show.legend = FALSE) +
geom_boxplot(show.legend = FALSE, alpha = 0.5) +
scale_color_viridis_d(option = "D", end = 0.8) +
scale_y_continuous(labels = label_percent()) +
theme_minimal() +
labs(
x = "Is the prognosticator alive?",
y = "Prediction accuracy for late winter/early spring",
title = "Accuracy of prognosticators predicting the coming season",
subtitle = "By living status of prognosticator"
)Multiple variables - Demo
Analyzing the relationship between three or more variables is called multivariate analysis.
- Facet the plot you created in the previous exercise by
forecaster_simple. Adjust labels accordingly.
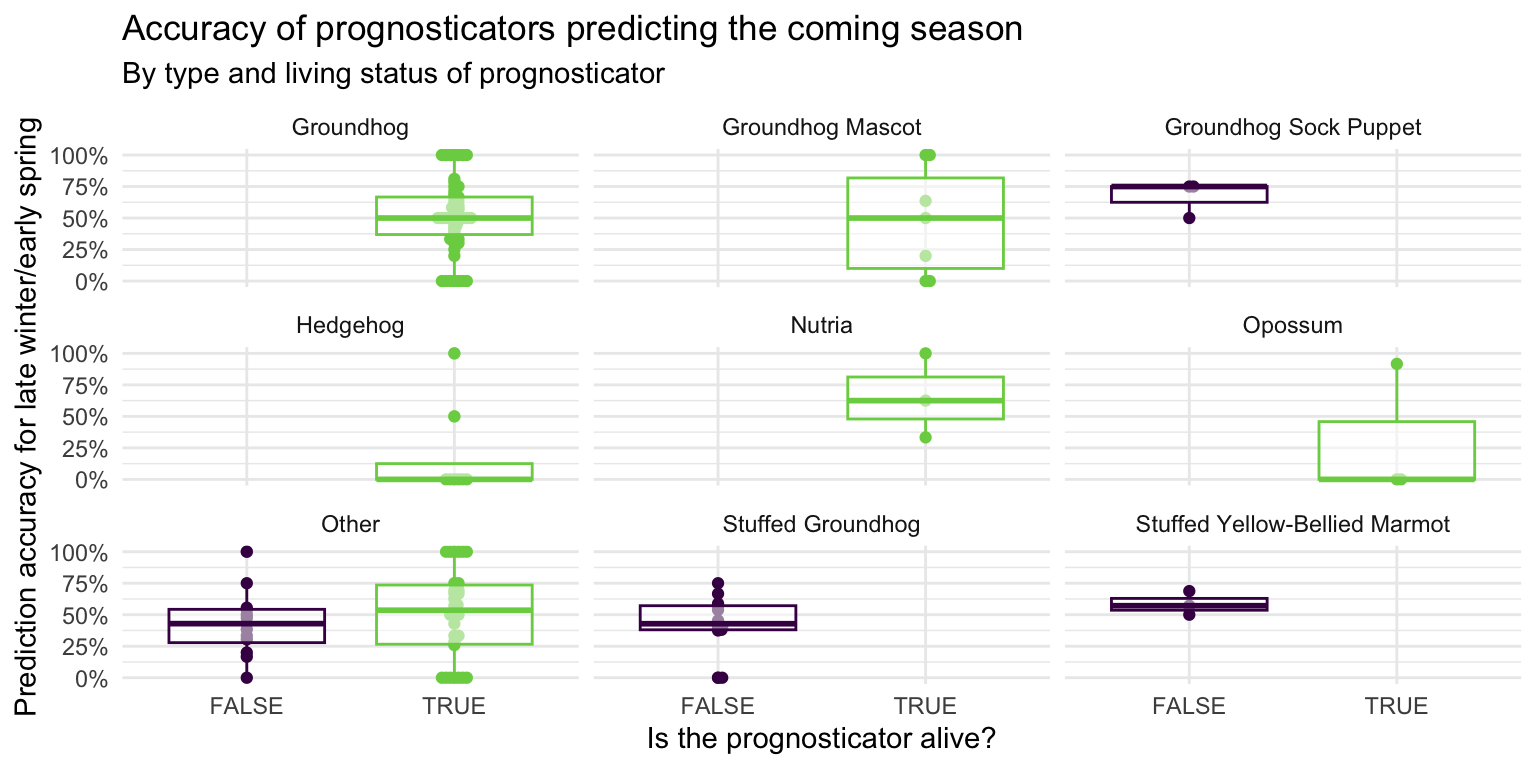
ggplot(
data = seers,
mapping = aes(x = alive, y = preds_rate, color = alive)
) +
geom_beeswarm(show.legend = FALSE) +
geom_boxplot(show.legend = FALSE, alpha = 0.5) +
scale_color_viridis_d(option = "D", end = 0.8) +
scale_y_continuous(labels = label_percent()) +
facet_wrap(vars(forecaster_simple)) +
theme_minimal() +
labs(
x = "Is the prognosticator alive?",
y = "Prediction accuracy for late winter/early spring",
title = "Accuracy of prognosticators predicting the coming season",
subtitle = "By type and living status of prognosticator"
)Before you continue, let’s turn off all warnings the code chunks generate and resize all figures. We’ll do this by editing the YAML.
Visualizing other variables - Your turn!
- Pick a single categorical variable from the data set and make a bar plot of its distribution.
# frequency count of forecaster_simple
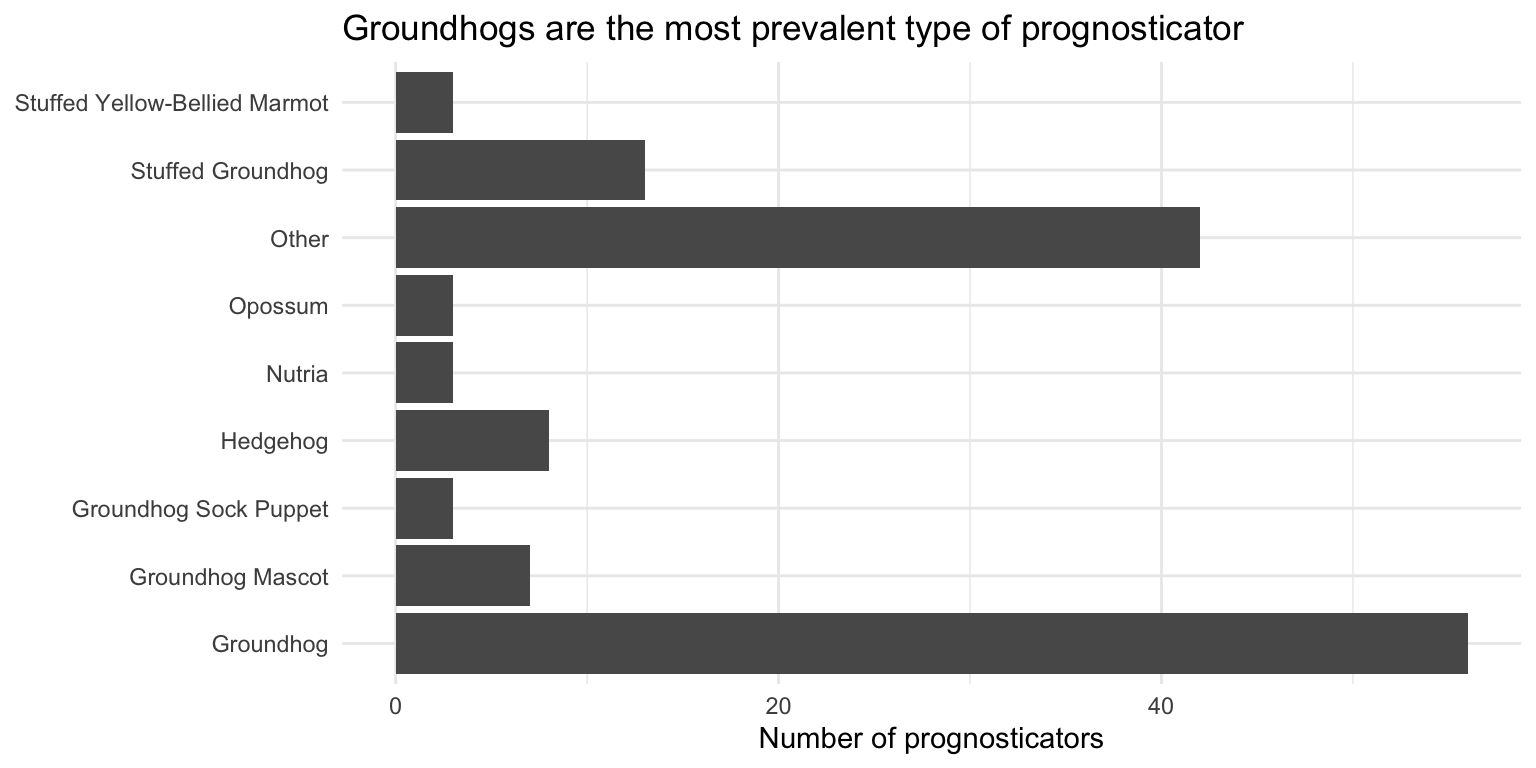
ggplot(data = seers, mapping = aes(y = forecaster_simple)) +
geom_bar() +
theme_minimal() +
labs(
title = "Groundhogs are the most prevalent type of prognosticator",
x = "Number of prognosticators",
y = NULL
)The \(y\)-axis is sorted alphabetically which doesn’t make a lot of sense, but fixing it requires some data wrangling (which we will learn next week!). Overall groundhogs are the most prevalent type of prognosticator.
- Pick two categorical variables and make a visualization to visualize the relationship between the two variables. Along with your code and output, provide an interpretation of the visualization.
# forecaster_simple vs. climate_region as a relative frequency bar chart
ggplot(data = seers, mapping = aes(y = forecaster_simple, fill = climate_region)) +
# position = "fill" makes the bars the same height
geom_bar(position = "fill") +
# percentage labeling
scale_x_continuous(labels = label_percent()) +
# use better color palette
scale_fill_brewer(type = "qual", palette = "Set1") +
theme_minimal() +
labs(
title = "Northeast is all about the groundhogs",
x = "Percentage of prognosticators",
y = NULL,
fill = "Climate region"
)# now as a count plot
ggplot(data = seers, mapping = aes(x = climate_region, y = forecaster_simple)) +
geom_count() +
labs(
title = "Northeast is all about the groundhogs",
x = "Climate region",
y = "Type of prognosticator",
size = "Number of\nprognosticators"
) +
theme_minimal() +
theme(legend.position = "bottom")It’s rather hard to visualize two categorical variables at once. The first plot shows the relative frequency of each type of prognosticator by climate region. The second plot shows the count of each type of prognosticator by climate region. Both plots show that the Northeast has a high proportion of groundhogs as prognosticators. Unfortunately we end up with overlapping labels on the second plot, while with the first graph we cannot tell the overall number of prognosticators by each type (everything is scaled to 100%).
- Make another plot that uses at least three variables. At least one should be numeric and at least one categorical. In 1-2 sentences, describe what the plot shows about the relationships between the variables you plotted. Don’t forget to label your code chunk.
ggplot(data = seers, mapping = aes(x = temp_mean, y = preds_long_winter_pct,
color = alive)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE) +
scale_x_continuous(
labels = label_number(suffix = "\u00b0F")
) +
scale_color_viridis_d(option = "D", end = 0.8) +
scale_y_continuous(labels = label_percent()) +
labs(
title = "Inanimate prognosticators are more likely to predict a long winter\nas average temperatures rise",
x = "Average temperature in February/March during pronosticators' 'lifetime'",
y = "Percentage of predictions for long winter",
color = "Is the prognosticator alive?"
) +
theme_minimal() +
theme(legend.position = "top")As average temperatures in February and March rise, inanimate prognosticators are associated with a higher likelihood of predicting a long winter. For living prognosticators, the relationship is less clear. The smoothing line is virtually flat, suggesting there is no association between average winter temperatures and whether or not the prognosticator predicts a long winter or early spring.
sessioninfo::session_info()─ Session info ───────────────────────────────────────────────────────────────
setting value
version R version 4.3.2 (2023-10-31)
os macOS Ventura 13.5.2
system aarch64, darwin20
ui X11
language (EN)
collate en_US.UTF-8
ctype en_US.UTF-8
tz America/New_York
date 2024-02-03
pandoc 3.1.1 @ /Applications/RStudio.app/Contents/Resources/app/quarto/bin/tools/ (via rmarkdown)
─ Packages ───────────────────────────────────────────────────────────────────
package * version date (UTC) lib source
beeswarm 0.4.0 2021-06-01 [1] CRAN (R 4.3.0)
bit 4.0.5 2022-11-15 [1] CRAN (R 4.3.0)
bit64 4.0.5 2020-08-30 [1] CRAN (R 4.3.0)
cli 3.6.2 2023-12-11 [1] CRAN (R 4.3.1)
colorspace 2.1-0 2023-01-23 [1] CRAN (R 4.3.0)
crayon 1.5.2 2022-09-29 [1] CRAN (R 4.3.0)
digest 0.6.34 2024-01-11 [1] CRAN (R 4.3.1)
dplyr * 1.1.4 2023-11-17 [1] CRAN (R 4.3.1)
evaluate 0.23 2023-11-01 [1] CRAN (R 4.3.1)
fansi 1.0.6 2023-12-08 [1] CRAN (R 4.3.1)
farver 2.1.1 2022-07-06 [1] CRAN (R 4.3.0)
fastmap 1.1.1 2023-02-24 [1] CRAN (R 4.3.0)
forcats * 1.0.0 2023-01-29 [1] CRAN (R 4.3.0)
generics 0.1.3 2022-07-05 [1] CRAN (R 4.3.0)
ggbeeswarm * 0.7.2 2023-04-29 [1] CRAN (R 4.3.0)
ggplot2 * 3.4.4 2023-10-12 [1] CRAN (R 4.3.1)
glue 1.7.0 2024-01-09 [1] CRAN (R 4.3.1)
gtable 0.3.4 2023-08-21 [1] CRAN (R 4.3.0)
here 1.0.1 2020-12-13 [1] CRAN (R 4.3.0)
hms 1.1.3 2023-03-21 [1] CRAN (R 4.3.0)
htmltools 0.5.7 2023-11-03 [1] CRAN (R 4.3.1)
htmlwidgets 1.6.4 2023-12-06 [1] CRAN (R 4.3.1)
jsonlite 1.8.8 2023-12-04 [1] CRAN (R 4.3.1)
knitr 1.45 2023-10-30 [1] CRAN (R 4.3.1)
labeling 0.4.3 2023-08-29 [1] CRAN (R 4.3.0)
lattice 0.21-9 2023-10-01 [1] CRAN (R 4.3.2)
lifecycle 1.0.4 2023-11-07 [1] CRAN (R 4.3.1)
lubridate * 1.9.3 2023-09-27 [1] CRAN (R 4.3.1)
magrittr 2.0.3 2022-03-30 [1] CRAN (R 4.3.0)
Matrix 1.6-1.1 2023-09-18 [1] CRAN (R 4.3.2)
mgcv 1.9-0 2023-07-11 [1] CRAN (R 4.3.2)
munsell 0.5.0 2018-06-12 [1] CRAN (R 4.3.0)
nlme 3.1-163 2023-08-09 [1] CRAN (R 4.3.2)
pillar 1.9.0 2023-03-22 [1] CRAN (R 4.3.0)
pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.3.0)
purrr * 1.0.2 2023-08-10 [1] CRAN (R 4.3.0)
R6 2.5.1 2021-08-19 [1] CRAN (R 4.3.0)
RColorBrewer 1.1-3 2022-04-03 [1] CRAN (R 4.3.0)
readr * 2.1.5 2024-01-10 [1] CRAN (R 4.3.1)
rlang 1.1.3 2024-01-10 [1] CRAN (R 4.3.1)
rmarkdown 2.25 2023-09-18 [1] CRAN (R 4.3.1)
rprojroot 2.0.4 2023-11-05 [1] CRAN (R 4.3.1)
rstudioapi 0.15.0 2023-07-07 [1] CRAN (R 4.3.0)
scales * 1.2.1 2024-01-18 [1] Github (r-lib/scales@c8eb772)
sessioninfo 1.2.2 2021-12-06 [1] CRAN (R 4.3.0)
stringi 1.8.3 2023-12-11 [1] CRAN (R 4.3.1)
stringr * 1.5.1 2023-11-14 [1] CRAN (R 4.3.1)
tibble * 3.2.1 2023-03-20 [1] CRAN (R 4.3.0)
tidyr * 1.3.0 2023-01-24 [1] CRAN (R 4.3.0)
tidyselect 1.2.0 2022-10-10 [1] CRAN (R 4.3.0)
tidyverse * 2.0.0 2023-02-22 [1] CRAN (R 4.3.0)
timechange 0.2.0 2023-01-11 [1] CRAN (R 4.3.0)
tzdb 0.4.0 2023-05-12 [1] CRAN (R 4.3.0)
utf8 1.2.4 2023-10-22 [1] CRAN (R 4.3.1)
vctrs 0.6.5 2023-12-01 [1] CRAN (R 4.3.1)
vipor 0.4.7 2023-12-18 [1] CRAN (R 4.3.1)
viridisLite 0.4.2 2023-05-02 [1] CRAN (R 4.3.0)
vroom 1.6.5 2023-12-05 [1] CRAN (R 4.3.1)
withr 2.5.2 2023-10-30 [1] CRAN (R 4.3.1)
xfun 0.41 2023-11-01 [1] CRAN (R 4.3.1)
yaml 2.3.8 2023-12-11 [1] CRAN (R 4.3.1)
[1] /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/library
──────────────────────────────────────────────────────────────────────────────Footnotes
I would prefer
prognosticators, but I had way too many typos preparing these materials to make you all use it.↩︎Source: Countdown to Groundhog Day. Application exercise inspired by Groundhogs Do Not Make Good Meteorologists originally published on FiveThirtyEight.↩︎
Prognosticators labeled as Animatronic/Puppet/Statue/Stuffed/Taxidermied are classified as not alive.↩︎
We adopt the same definition as FiveThirtyEight. An “Early Spring” is defined as any year in which the average temperature in either February or March was higher than the historic average. A “Late Winter” was when the average temperature in both months was lower than or the same as the historical average.↩︎