library(tidyverse)
library(scales)
library(rvest)Lab 04 - Money in U.S. politics
This lab is due March 11 at 11:59pm.
Learning goals
In this lab, you will…
- use web scraping to import unstructured data from HTML files
- write a function to perform repetitive operations efficiently
- create an iterative operation to apply a function to multiple inputs
- clean variables for data analysis
Money in politics
Every election cycle brings its own brand of excitement – and lots of money. Political donations are of particular interest to political scientists and other researchers studying politics and voting patterns. They are also of interest to citizens who want to stay informed of how much money their candidates raise and where that money comes from.
In the United States, “only American citizens (and immigrants with green cards) can contribute to federal politics, but the American divisions of foreign companies can form political action committees (PACs) and collect contributions from their American employees.”1
In this assignment we will scrape and work with data on foreign-connected PACs that donate to US political campaigns. First, we will get data on foreign-connected PAC contributions in the 2022 election cycle. Then, you will use a similar approach to get data such contributions from previous years so that we can examine trends over time.
In order to complete this assignment you will need a browser with the Selector Gadget extension installed.
Getting started
Go to the info2950-sp24 organization on GitHub. Click on the repo with the prefix lab-04. It contains the starter documents you need to complete the lab.
Clone the repo and start a new project in RStudio. See the Lab 0 instructions for details on cloning a repo and starting a new R project.
First, open the Quarto document
lab-04.qmdand Render it.Make sure it compiles without errors.
All team members should clone the team GitHub repository for the lab. Then, one team member should edit the document YAML by adding the team name to the subtitle field and adding the names of the team members contributing to lab to the author field. Hopefully that’s everyone, but if someone doesn’t contribute during the lab session or throughout the week before the deadline, their name should not be added. If you have 4 members in your team, you can delete the line for the 5th team member. Then, this team member should render the document and commit and push the changes. All others should not touch the document at this stage.
title: "Lab 04 - Money in U.S. politics"
subtitle: "Team name"
author:
- "Team member 1 (netID)"
- "Team member 2 (netID)"
- "Team member 3 (netID)"
- "Team member 4 (netID)"
- "Team member 5 (netID)"
date: today
format: pdfWarm up
Before we introduce the data, let’s warm up with some simple exercises.
- Update the YAML, changing the author name to your name, and render the document.
- Commit your changes with a meaningful commit message.
- Push your changes to GitHub.
- Go to your repo on GitHub and confirm that your changes are visible in your
.qmdand .pdffiles. If anything is missing, render, commit, and push again.
Packages
We’ll use the tidyverse package for much of the data wrangling, the scales package for better plot labels, and rvest for web scraping. These packages are already installed for you. You can load it by running the following in your Console:
Data collection via web scraping
Pick a member of the team to complete exercise 1. All others should contribute to the discussion but only one person should type up the answer, run the R script, commit, and push to GitHub. All others should not touch the document.
The data come from OpenSecrets.org, a “website tracking the influence of money on U.S. politics, and how that money affects policy and citizens’ lives”. This website is hosted by The Center for Responsive Politics, which is a nonpartisan, independent nonprofit that “tracks money in U.S. politics and its effect on elections and public policy.”2
Before getting started, let’s check that a bot has permissions to access pages on this domain.
library(robotstxt)
paths_allowed("https://www.opensecrets.org")[1] TRUEExercise 1
Our goal is to scrape data for contributions in all election years Open Secrets has data for. Since that means repeating a task many times, let’s first write a function that works on the first page. Confirm it works on a few others. Then iterate it over pages for all years.
Complete the following set of steps in the lab-04-scrape-pacs.R file in your repository. This file already contains some starter code to help you out.
Write a function called
scrape_pac()that scrapes information from the Open Secrets webpage for foreign-connected PAC contributions in a given year. This function should- have one input: the URL of the webpage and should return a data frame.
- rename variables scraped, using
snake_casenaming. - clean up the Name variable to remove extraneous whitespace characters.
- add a new column to the data frame for
year. We will want this information when we ultimately have data from all years, so this is a good time to keep track of it. Our function doesn’t take a year argument, but the year is embedded in the URL, so we can extract it out of there, and add it as a new column. Use thestr_sub()function to extract the last 4 characters from the URL. You will probably want to look at the help for this function to figure out how to specify “last 4 characters”.
Define the URLs for 2022, 2020, and 2000 contributions. Then, test your function using these URLs as inputs. Does the function seem to do what you expected it to do?
Construct a vector called
urlsthat contains the URLs for each webpage that contains information on foreign-connected PAC contributions for a given year. Identify all election years available on Money in Politics.Map the
scrape_pac()function overurlsin a way that will result in a data frame calledpac_all.Write the data frame to a csv file called
pac-all.csvin thedatafolder.
After the team member working on Exercise 1 runs the script, commits, and pushes, another team member should pull their changes and run the script again to verify correct output. Then, they should write the answer to Exercise 2-3. All others should contribute to the discussion but only one person should type up the answer, render the document, commit, and push to GitHub. All others should not touch the document.
Data cleaning
For the remaining exercises, complete them in the lab-04.qmd file in your repository.
In your Quarto document, load pac-all.csv and report its number of observations and variables using inline code.
In this section we clean the pac_all data frame to prepare it for analysis and visualization. We have two goals in data cleaning:
Separate the
country_parentinto two such that country and parent company appear in different columns for country-level analysis.Convert contribution amounts in
total,dems, andrepubsfrom character strings to numeric values.
The following exercises walk you through how to make these fixes to the data.
Exercise 2
Separate country_parent into country and parent columns. Note that country and parent company names are separated by / (which will need to be specified in your function) and also note that there are some entries where the / sign appears twice and in these cases we want to only split the value at the first occurrence of /. This can be accomplished by setting the too_many argument to "merge" so that the cell is split into only 2 segments, e.g. we want "Denmark/Novo Nordisk A/S" to be split into "Denmark" and "Novo Nordisk A/S". (See help for the appropriate separate_*() function for more on this.) End your code chunk by printing out the top 10 rows of your data frame (if you just type the data frame name it should automatically do this for you).
Exercise 3
Remove the character strings including $ and , signs in the total, dems, and repubs columns and convert these columns to numeric.
parse_number()will need some help here. Be sure to check your output and make sure there were no parsing failures if you use it to convert the column. If so, rewrite your code to avoid them.- The
$character is a special character so it will need to be escaped.
End your code chunk by printing out the top 10 rows of your data frame (if you just type the data frame name it should automatically do this for you).
After the team member working on Exercises 2-3 renders, commits, and pushes, another team member should pull their changes and render the document. Then, they should write the answer to Exercise 4. All others should contribute to the discussion but only one person should type up the answer, render the document, commit, and push to GitHub. All others should not touch the document.
Data visualization and interpretation
Exercise 4
Create a line plot of total contributions from all foreign-connected PACs in Canada and Mexico over the years. Once you have made the plot, write a brief interpretation of what the graph reveals.
- Filter for only
CanadaandMexico. - Calculate sum of total contributions from PACs for each year for each country by using a sequence of
group_by()thensummarize(). - Make a plot of year (x-axis) by total contributions (y-axis) where two lines identified by different colors represent each of Canada and Mexico.
After the team member working on Exercises 4 renders, commits, and pushes, another team member should pull their changes and render the document. Then, they should write the answer to Exercise 5. All others should contribute to the discussion but only one person should type up the answer, render the document, commit, and push to GitHub. All others should not touch the document.
Exercise 5
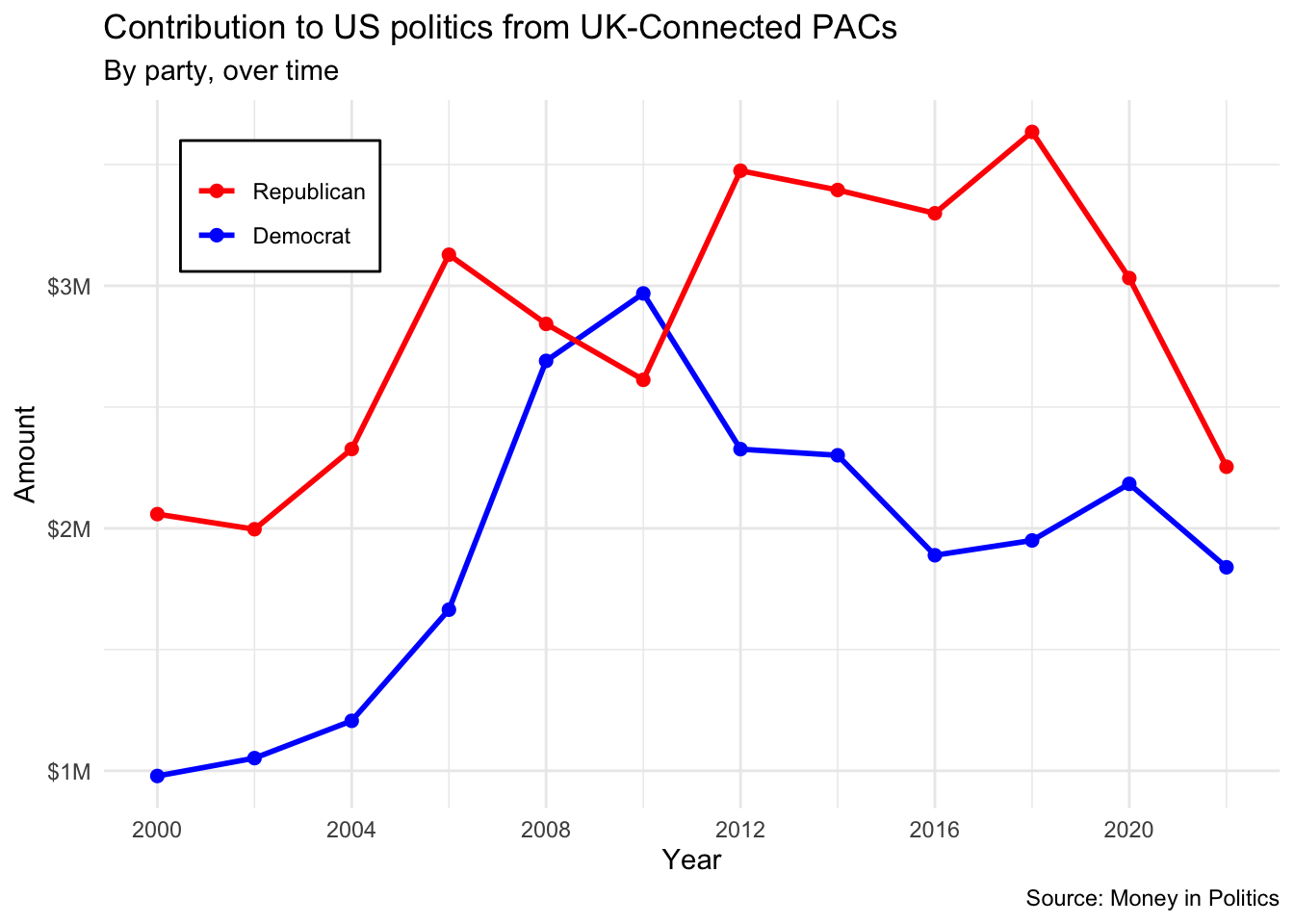
Recreate the following visualization. Once you have made the plot, write a brief interpretation of what the graph reveals. Note that these are only contributions from the United Kingdom.
Note: The figure you create might look slightly different than this one if the data on the website has been updated recently.
After the team member working on Exercise 5 renders, commits, and pushes, all other team members should pull the changes and render the document. Finally, a team member different than the one responsible for typing up responses to Exercise 5 should do the last task outlined below.
Submission
Once you are finished with the lab, you will submit your final PDF document to Gradescope.
Before you wrap up the assignment, make sure all documents are updated on your GitHub repo. We will be checking these to make sure you have been practicing how to commit and push changes.
You must turn in a PDF file to the Gradescope page by the submission deadline to be considered “on time”.
To submit your assignment:
- Go to http://www.gradescope.com and click Log in in the top right corner.
- Click School Credentials \(\rightarrow\) Cornell University NetID and log in using your NetID credentials.
- Click on your INFO 2950 course.
- Click on the assignment, and you’ll be prompted to submit it.
- Mark all the pages associated with exercise. All the pages of your lab should be associated with at least one question (i.e., should be “checked”).
- Select all pages of your .pdf submission to be associated with the “Workflow & formatting” question.
Grading
| Component | Points |
|---|---|
| Ex 1 | 15 |
| Ex 2 | 8 |
| Ex 3 | 7 |
| Ex 4 | 6 |
| Ex 5 | 9 |
| Workflow & formatting | 5 |
| Total | 50 |
The “Workflow & formatting” component assesses the reproducible workflow. This includes:
- Having at least 3 informative commit messages
- Each team member contributing to the repo with commits at least once
- Following tidyverse code style
- All code being visible in rendered PDF (no more than 80 characters)
Acknowledgments
- This assignment is derived from Data Science in a Box and licensed under CC BY-SA 4.0.
Footnotes
Source: Open Secrets - About.↩︎